Comparison of Euler and Euler-Cromer Numerical Methods for Undamped and Damped Spring Oscillation
DOI:
https://doi.org/10.12928/irip.v4i2.4803Keywords:
Damped Oscillation, Undamped Oscillation, Euler Method, Euler-Cromer MethodAbstract
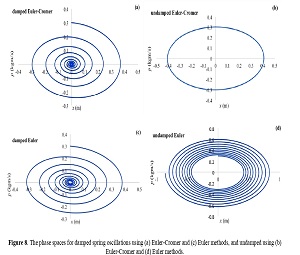
This study aimed to numerically analyze damped and undamped oscillations of a spring using the Euler and Euler-Cromer methods via Spreadsheet software. The varied parameters in this study were the damping constant, namely 0.1 (damped) and 0.0 (undamped). Various quantities analyzed in this study were position (x), velocity (v), kinetic energy (K), potential energy (U), mechanical energy (E), and phase space as a function of time (t). Iteration was done in t < 60-time steps (seconds). The results of this study indicated that when the spring experiences damping, the numerical results of x, v, K, U, E, and the phase space decrease periodically to zero due to the damping force, both for the Euler and Euler-Cromer methods. Meanwhile, for the undamped spring (zero damping constant), there was a difference in the results for the Euler and Euler-Cromer methods. For the Euler method, the resulting values of x, v, K, U, E, and the phase space increased periodically with time, which was not following the actual situation. According to the simple harmonic oscillation, the Euler-Cromer method values of x, v, K, U, E, and the phase space were stable over time.
References
R. F. Martin, “Undergraduate Computation Physics Education: Uneven History and Promising Future,” XXVII IUPAP, Conference on Computational Physics (CCP2015) 2-5 December 2015, J Phys. Conf. Ser., vol. 759, p. 012005, 2016. doi: 10.1088/1742-6596/759/1/012005.
X. Wang, C. Guo, D. A. Yuen, and G. Luo, “GeoVReality: A Computational Interactive Virtual Reality Visualization Framework and Workflow for Geophysical Research,” Physics of the Earth and Planetary Interiors, vol. 298, p. 106312, 2020. doi: 10.1016/j.pepi.2019.106312.
M. Bansal, S. Bansal, and R. Kumar, “A Simulation of Two-Body Decay of A Particle and Radioactive Equilibrium States,” Physics Education, vol. 56(5), p. 055007, 2021. doi: 10.1088/1361-6552/ac0159.
N. B. Otojonova and D. B. Tojonova, “The Role of Differential Equation in Physical Exercise,” Pedagogy & Physchology: Theory and Practice, vol. 4(30), pp. 26–30, 2020. https://journals.indexcopernicus.com/api/file/viewByFileId/1222945.pdf
T. Rabczuk, H. Ren, and X. Zhuang, “A Nonlocal Operator Method for Partial Differential Equations With Application to Electromagnetic Waveguide Problem,” Computers, Materials, & Continua, vol. 59(1), pp. 31-55, 2019. doi: 10.32604/cmc.2019.04567.
R. D. Kaufman, “A First Law Through Experiment With A Second Law Result of Heat Engines Based on A Self-Contained Modified Carnot Cycle,” European Jornal of Physics Education, vol. 10(1), pp. 24–37, 2019. doi: 10.20208/ejpe.v10i1.222.
V. M. Tapilin, “Solving the Schrodinger Equation for Helium-Like Ions With the Method of Configuration Weight Functions,” Journal of Structural Chemistry., vol. 60, pp. 1–6, 2019. doi: 10.1134/S0022476619010013.
J. Li, N. D. Drumond, P. Schuck, and V. Olevano, “Comparing Many-Body Approaches Against the Helium Atom Exact Solution,” SciPost Phys., vol. 6, p. 040, 2019. doi: 10.21468/SciPostPhys.6.4.040.
D. C. Giancoli, Fisika: Prinsip dan Aplikasi Jilid 2 [Physics: Principles with Application], Ed. 7. Jakarta: Erlangga, 2014.
M. R. Aulia, “Osilasi Teredam pada Pegas dengan Medium Fluida [Damped Oscillations in A Spring With A Fluid Medium],” Journal of Teaching and Learning Physics, vol. 3(1), pp. 22–26, 2018. doi: 10.15575/jotalp.v3i1.6549.
J. Poonyawatpornkul and P. Wattankasiwich, “High-Speed Video Analysis of Damped Harmonic Motion,” Physics Education, vol. 48(6), pp. 782-789, 2013. doi: 10.1088/0031-9120/48/6/782.
A. Fauzi, “Analisis Gerak Harmonik Teredam (Damped Harmonic Motion) dengan Spreadsheet Excel [Analysis of Damped Harmonic Motion (Damped Harmonic Motion) With an Excel Spreadsheet],” Orbith, vol. 7(2), pp. 318–322, 2011. https://eprints.uns.ac.id/1713/.
A. Nurdin and S. Hastuti, “Analsis Gerak Osilator Harmonik Teredam Menggunakan Metode Numerik [Analysis of Damped Harmonic Oscillator Motion Using Numerical Method],” Journal of Mechanical Engineering, vol. 3(2), pp. 13-19, 2019. doi: 10.31002/jom.v3i2.3366.
R. Eso, “Simulasi Gerak Osilasi Paksa dengan Redaman Menggunakan Spreadsheet Excel dan Macro Visual Basic for Application [Simulation of Forced Oscillation Motion With Damping Using Excel Spreadsheet and Macro Visual Basic for Application],” Jurnal Aplikasi Fisika, vol. 13(3), pp. 52-55, 2017. http://ojs.uho.ac.id/index.php/JAF/article/view/4141/3228
D. U. Sowarno, “Getaran Osilasi Teredam pada Pendulum dengan Magnet dan Batang Aluminium [Damped Oscillating Vibrations on A Pendulum With Magnets and Aluminum Rods],” In Seminar Kontribusi Fisika, ITB, Bandung 2015.
S. Li, P. Xiang, B. Wei, C. Zuo, L. Jiang, and W. He, “Interface Friction Effects on Scaling A Vertical Spring-Viscous Damper Isolation System in A Shaking Table Test,” Structures, vol. 33, pp. 1878-1891, 2021. doi: 10.1016/j.istruc.2021.05.046.
N. Maus and F. Gordaninejad, “A Bi-Diretional, Liquid-Spring-Magnetorheological-Fluid-Damper System,” Frontiers in Materials, vol. 6 (6), pp. 1-11, 2019. doi: 10.3389/fmats.2019.00006.
Downloads
Published
Issue
Section
License
Copyright (c) 2021 Nurul Miftakhul Janah, Fajrul Falah, Ratnawati, Ishafit, Wipsar Sunu Brams Dwandaru

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Authors who publish in IRiP agree to the following terms: Authors retain copyright and grant the IRiP right of first publication with the work simultaneously licensed under a Creative Commons Attribution License (CC BY-SA 4.0) that allows others to share (copy and redistribute the material in any medium or format) and adapt (remix, transform, and build upon the material) the work for any purpose, even commercially with an acknowledgment of the work's authorship and initial publication in IRiP. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial publication in IRiP. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See The Effect of Open Access).














