The Ground State Energy of Helium Using Hartree-Fock Roothaan With Six Expansion Terms of Gaussian Type Orbital (GTO-6G)
DOI:
https://doi.org/10.12928/irip.v4i1.3862Keywords:
Gaussian Type Orbital, Hartree-Fock Roothaan, Helium, Six Expansion, Ground-state EnergyAbstract
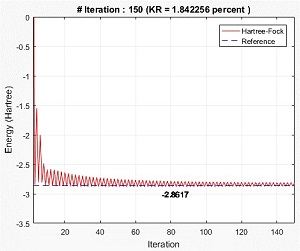
An implementation of the Hartree-Fock Roothaan with six expansion terms of Gaussian Type Orbitals (GTO-6G) is described and used to study the Helium atom’s ground state accurately. The objective of this research is to calculate the ground state energy of the Helium atom. The analysis was conducted using the numerical method using Matlab2017b. By using the Hartree-Fock Roothaan method, the complexity of Hartree-Fock in integrating the differential equations of eigenvalues for each electron is repeatedly successfully overcome by expressing Hartree-Fock orbitals in the form of linear combinations, known as STO (Slater Type Orbitals) and GTO (Gaussian Type Orbital). The Hartree-Fock Roothaan approximation procedure begins by assigning an initial guess value to the elements of the density matrices and then constructing the first Fock matrix from these matrices. The calculation is performed using the various iterations in multiples of 50, show that the error value expressed in relative uncertainty is getting smaller at the 150th iteration, which is around 1.84%. Compared with some literature, the relative uncertainty value is still within tolerance (below 5%). The contribution of theoretical implications in this study can be used as input for other researchers to review the Hartree-Fock Roothaan method and improve accuracy.
References
[2] P. W. Atkins and R. S. Friedman, Molecular Quantum Mechanics, 5th ed. USA: Oxford University Press, 2011.
[3] A. Flores-Riveros, N. Aquino, and H. E. Montgomery, “Spherically compressed helium atom described by perturbative and variational methods,†Phys. Lett. A, vol. 374, no. 10, pp. 1246–1252, Feb. 2010, doi: 10.1016/j.physleta.2009.12.062.
[4] N. Zettili, Quantum Mechanics: Concepts and Applications, 2nd ed. Chichester, U.K: John Wiley & Sons, Inc, 2009.
[5] N. Azis, F. Bidalo, and Z. Su’ud, “Penentuan Energi Dasar Atom Berilium (Be) Menggunakan Metode Variasional Dengan Dua Parameter [Determination of the Basic Energy of Beryllium (Be) Atoms Using Variational Methods with Two Parameters],†Saintifik, vol. 6, no. 1, pp. 79–84, Jun. 2020, doi: 10.31605/saintifik.v6i1.235.
[6] R. Custodio, G. de Souza Tavares de Morais, and M. G. Rodrigues, “A Grid-based Variational Method to the Solution of the Schrödinger Equation: The Q-exponential and the Near Hartree-Fock Results for the Ground State Atomic Energies,†J. Mol. Model., vol. 24, no. 7, p. 188, Jul. 2018, doi: 10.1007/s00894-018-3715-7.
[7] I. N. Eremkin, Y. B. Malykhanov, and M. V Gorshunov, “Calculation of Energies of the Isoelectronic Series of Atoms (Z ≤ 29) Using the Hartree–Fock Method,†in Journal of Physics: Conference Series, Aug. 2016, vol. 735, p. 012052, doi: 10.1088/1742-6596/735/1/012052.
[8] A. W. King, A. L. Baskerville, and H. Cox, “Hartree–Fock Implementation Using a Laguerre-Based Wave Function for the Ground State and Correlation Energies of Two-Electron Atoms,†Philos. Trans. R. Soc. A Math. Phys. Eng. Sci., vol. 376, no. 2115, p. 20170153, Mar. 2018, doi: 10.1098/rsta.2017.0153.
[9] M. Hjorth-Jensen, M. P. Lombardo, and U. van Kolck, Eds., An Advanced Course in Computational Nuclear Physics, vol. 936. Cham: Springer International Publishing, 2017.
[10] H. G. A. Burton, “Hartree–Fock Critical Nuclear Charge in Two-Electron Atoms,†J. Chem. Phys., vol. 154, no. 11, p. 111103, Mar. 2021, doi: 10.1063/5.0043105.
[11] M. O. Tjia. and I. M. Sutjahja, Orbital Kuantum: Pengantar Teori dan Contoh Aplikasinya [Quantum Orbitals: An Introduction to Theory and Examples of Its Application]. Bandung: Karya Putra Darmawati Bandung, 2012.
[12] A. I. Ahmadov, F. G. Pashaev, D. B. Bairamova, and A. G. Gasanov, “Calculation of the Energy of the Interelectron Interaction in Molecules in a Basis of Slater Functions,†Russ. Phys. J., vol. 61, no. 10, pp. 1848–1854, Feb. 2019, doi: 10.1007/s11182-019-01608-z.
[13] L. P. A. Krisnaa, N. L. Rizkiyahb, F. H. Murdakac, N. Amalia, and I. M. Sutjahja, “Optimasi Eksponen Orbital Slater Dua Suku untuk Keadaan Dasar Elektron Atom Helium Berdasarkan Metode Hartree-Fock-Roothaan dalam Mathematica® [Optimization of the Two-Term Slater Orbital Exponent for the Electron Ground State of Helium Atoms Based on the Hartree-Fock-Roothaan Method in Mathematica®],†in Prosiding Seminar Kontribusi Fisika, 2018, pp. 166–173.
[14] J. Li, N. D. Drummond, P. Schuck, and V. Olevano, “Comparing Many-Body Approaches Against the Helium Atom Exact Solution,†SciPost Phys., vol. 6, no. 4, p. 040, Apr. 2019, doi: 10.21468/SciPostPhys.6.4.040.
[15] A. E. Feiguin, “Phys 5870: Modern Computational Methods in Solids,†Northeastern University, 2012.
[16] E. BuendÃa, F. J. Gálvez, and A. Sarsa, “Hartree–Fock wave functions with a modified GTO basis for atoms,†Int. J. Quantum Chem., vol. 65, no. 1, pp. 59–64, 1997, doi: 10.1002/(SICI)1097-461X(1997)65:1<59::AID-QUA6>3.0.CO;2-%23.
[17] Y. Chen, L. Zhang, H. Wang, and W. E, “Ground State Energy Functional With Hartree–Fock Efficiency and Chemical Accuracy,†J. Phys. Chem. A, vol. 124, no. 35, pp. 7155–7165, Sep. 2020, doi: 10.1021/acs.jpca.0c03886.
[18] E. V. Ludeña, “SCF Hartree–Fock Calculations of Ground State Wavefunctions of Compressed Atoms,†J. Chem. Phys., vol. 69, no. 4, pp. 1770–1775, Aug. 1978, doi: 10.1063/1.436710.
[19] Y. Tsubono, “Calculation of Helium Ground State Energy by Bohr’s Theory-Based Methods,†arXiv Prepr. arXiv0903.2546, 2009.
[20] S. A. Ekong, M. T. Oloyede, and D. A. Oyegoke, “Ground-State Energy Calculation of Helium Atom Using Quantum Monte Carlo CASINO-Code,†Adv. Phys. Theor. Appl., vol. 46, pp. 1–6, 2015.
[21] S. Purwaningsih, P. Nurwantoro, and A. Hermanto, “Calculation of Ground State Energy of Helium Using Hylleraas Trial Function Expansion,†Int. J. Eng. Res. Technol., vol. 12, no. 8, pp. 1178–1182, 2019.
[22] S. B. Doma, M. O. Shaker, A. M. Farag, and F. N. El-Gammal, “Ground States of Helium Atom and Hydrogen Negative Ion in the Presence of Magnetic Field Using Variational Monte Carlo Technique,†Acta Phys. Pol. A, vol. 126, no. 3, pp. 700–705, Aug. 2014, doi: 10.12693/APhysPolA.126.700.
Downloads
Published
Issue
Section
License
Copyright (c) 2021 Nurlina, Fitriah Bidalo

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Authors who publish in IRiP agree to the following terms: Authors retain copyright and grant the IRiP right of first publication with the work simultaneously licensed under a Creative Commons Attribution License (CC BY-SA 4.0) that allows others to share (copy and redistribute the material in any medium or format) and adapt (remix, transform, and build upon the material) the work for any purpose, even commercially with an acknowledgment of the work's authorship and initial publication in IRiP. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial publication in IRiP. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See The Effect of Open Access).














