Hybrid ABC–K Means for Optimal Cluster Number Determination in Unlabeled Data

Authors

Harunur Rosyid Universitas Muhammadiyah Gresik
Muhammad Modi bin Lakulu Universiti Pendidikan Sultan Idris Malaysia
Ramlah bt. Mailok Universiti Pendidikan Sultan Idris Malaysia

DOI:

https://doi.org/10.12928/mf.v6i2.11529

Abstract

This study presents the ABC K Means GenData algorithm, an enhancement over traditional K Means clustering that integrates the Artificial Bee Colony (ABC) optimization approach. The ABC K Means GenData algorithm addresses the issue of local optima commonly encountered in standard K Means algorithms, offering improved exploration and exploitation strategies. By utilizing the dynamic roles of employed, onlooker, and scout bees, this approach effectively navigates the clustering space for categorical data. Performance evaluations across several datasets demonstrate the algorithm's superiority. For the Zoo dataset, ABC K Means GenData achieved high Accuracy (0.8399), Precision (0.8089), and Recall (0.7286), with consistent performance compared to K Means and Fuzzy K Means. Similar results were observed for the Breast Cancer dataset, where it matched the Accuracy and Precision of K Means and surpassed Fuzzy K Means in Precision and Recall. In the Soybean dataset, the algorithm also performed excellently, showing top scores in Accuracy, Precision, Recall, and Rand Index (RI), outperforming both K Means and Fuzzy K Means.. The comprehensive results indicate that ABC K Means GenData excels in clustering categorical data, providing robust and reliable performance. Future research will explore its application to mixed data types and social media datasets, aiming to further optimize clustering techniques.

References

A. K. Jain, M. N. Murty, and P. J. Flynn, “Data Clustering: A Review,” 2000.

I. S. Dhillon, “Co-clustering documents and words using bipartite spectral graph partitioning,” in Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, in KDD ’01. New York, NY, USA: Association for Computing Machinery, 2001, pp. 269–274. doi: 10.1145/502512.502550.

J. Macqueen, “SOME METHODS FOR CLASSIFICATION AND ANALYSIS OF MULTIVARIATE OBSERVATIONS,” vol. 233, no. 233, pp. 281–297.

S. Lloyd, “Least squares quantization in PCM,” IEEE Trans Inf Theory, vol. 28, no. 2, pp. 129–137, 1982, doi: 10.1109/TIT.1982.1056489.

X. Wu and V. Kumar, The Top Ten Algorithms in Data Mining. 2009.

J. A. Hartigan and M. A. Wong, “Algorithm AS 136: A K-Means Clustering Algorithm,” 1979.

D. Karaboğa, “AN IDEA BASED ON HONEY BEE SWARM FOR NUMERICAL OPTIMIZATION,” 2005. [Online]. Available: https://api.semanticscholar.org/CorpusID:8215393

D. Karaboga and B. Basturk, “On the performance of artificial bee colony (ABC) algorithm,” Appl Soft Comput, vol. 8, no. 1, pp. 687–697, 2008, doi: https://doi.org/10.1016/j.asoc.2007.05.007.

J. Redha and J. Redha Mutar, “A Review of Clustering Algorithms,” International Journal of Computer Science and Mobile Applications, vol. 10, pp. 44–50, 2022, doi: 10.5281/zenodo.7243829.

S. Naeem, A. Ali, S. Anam, and M. M. Ahmed, “An Unsupervised Machine Learning Algorithms: Comprehensive Review,” International Journal of Computing and Digital Systems, vol. 13, no. 1, pp. 911–921, 2023, doi: 10.12785/ijcds/130172.

Y. Chen et al., “Fast density peak clustering for large scale data based on kNN,” Knowl Based Syst, vol. 187, p. 104824, 2020, doi: https://doi.org/10.1016/j.knosys.2019.06.032.

T. A. Khan and S. H. Ling, “A novel hybrid gravitational search particle swarm optimization algorithm,” Eng Appl Artif Intell, vol. 102, p. 104263, 2021, doi: https://doi.org/10.1016/j.engappai.2021.104263.

X. Pan, Y. Wang, Y. Lu, and N. Sun, “Improved artificial bee colony algorithm based on two-dimensional queue structure for complex optimization problems,” Alexandria Engineering Journal, vol. 86, pp. 669–679, 2024, doi: https://doi.org/10.1016/j.aej.2023.12.011.

Z. Zhang, J. Lan, and Z. Zhang, “K-means clustering algorithm based on bee colony strategy,” in Journal of Physics: Conference Series, IOP Publishing Ltd, Sep. 2021. doi: 10.1088/1742-6596/2031/1/012058.

I. Arfiani, H. Yuliansyah, and M. D. Suratin, “Implementasi Bee Colony Optimization Pada Pemilihan Centroid (Klaster Pusat) Dalam Algoritma K-Means,” Building of Informatics, Technology and Science (BITS), vol. 3, no. 4, pp. 756–763, Mar. 2022, doi: 10.47065/bits.v3i4.1446.

B. Zhou, B. Lu, and S. Saeidlou, “A Hybrid Clustering Method Based on the Several Diverse Basic Clustering and Meta-Clustering Aggregation Technique,” Cybern Syst, vol. 55, no. 1, pp. 203–229, 2024, doi: 10.1080/01969722.2022.2110682.

S. Ghosh and S. K. Dubey, “Comparative Analysis of K-Means and Fuzzy C-Means Algorithms,” 2013. [Online]. Available: www.ijacsa.thesai.org

Q. Tan, H. Wu, B. Hu, and X. Liu, “An improved Artificial Bee Colony algorithm for clustering,” in GECCO 2014 - Companion Publication of the 2014 Genetic and Evolutionary Computation Conference, Association for Computing Machinery, 2014, pp. 19–20. doi: 10.1145/2598394.2598464.

W. Shenghui and L. Hanbing, “Adaptive K-valued K-means clustering algorithm,” in 2020 5th International Conference on Mechanical, Control and Computer Engineering (ICMCCE), 2020, pp. 1442–1445. doi: 10.1109/ICMCCE51767.2020.00316.

T. Sadhu, S. Chowdhury, S. Mondal, J. Roy, J. Chakrabarty, and S. K. Lahiri, “A COMPARATIVE STUDY OF METAHEURISTICS ALGORITHMS BASED ON THEIR PERFORMANCE OF COMPLEX BENCHMARK PROBLEMS,” Decision Making: Applications in Management and Engineering, vol. 6, no. 1, pp. 341–364, Apr. 2023, doi: 10.31181/dmame0306102022r.

S. Zhu, L. Xu, and E. D. Goodman, “Evolutionary multi-objective automatic clustering enhanced with quality metrics and ensemble strategy,” Knowl Based Syst, vol. 188, p. 105018, 2020, doi: https://doi.org/10.1016/j.knosys.2019.105018.

M. A. Damos et al., “Enhancing the K-Means Algorithm through a Genetic Algorithm Based on Survey and Social Media Tourism Objectives for Tourism Path Recommendations,” ISPRS Int J Geoinf, vol. 13, no. 2, Feb. 2024, doi: 10.3390/ijgi13020040.

N. Kaur and S. Aggarwal, “Comparative Analysis of Hybrid K-Mean Algorithms on Data Clustering,” 2017. [Online]. Available: www.ijcat.com384

S. Liu and Y. Zou, “An improved hybrid clustering algorithm based on particle swarm optimization and K-means,” in IOP Conference Series: Materials Science and Engineering, Institute of Physics Publishing, Mar. 2020. doi: 10.1088/1757-899X/750/1/012152.

M. Zhao, X. Song, and S. Xing, “Improved Artificial Bee Colony Algorithm with Adaptive Parameter for Numerical Optimization,” Applied Artificial Intelligence, vol. 36, no. 1, 2022, doi: 10.1080/08839514.2021.2008147.

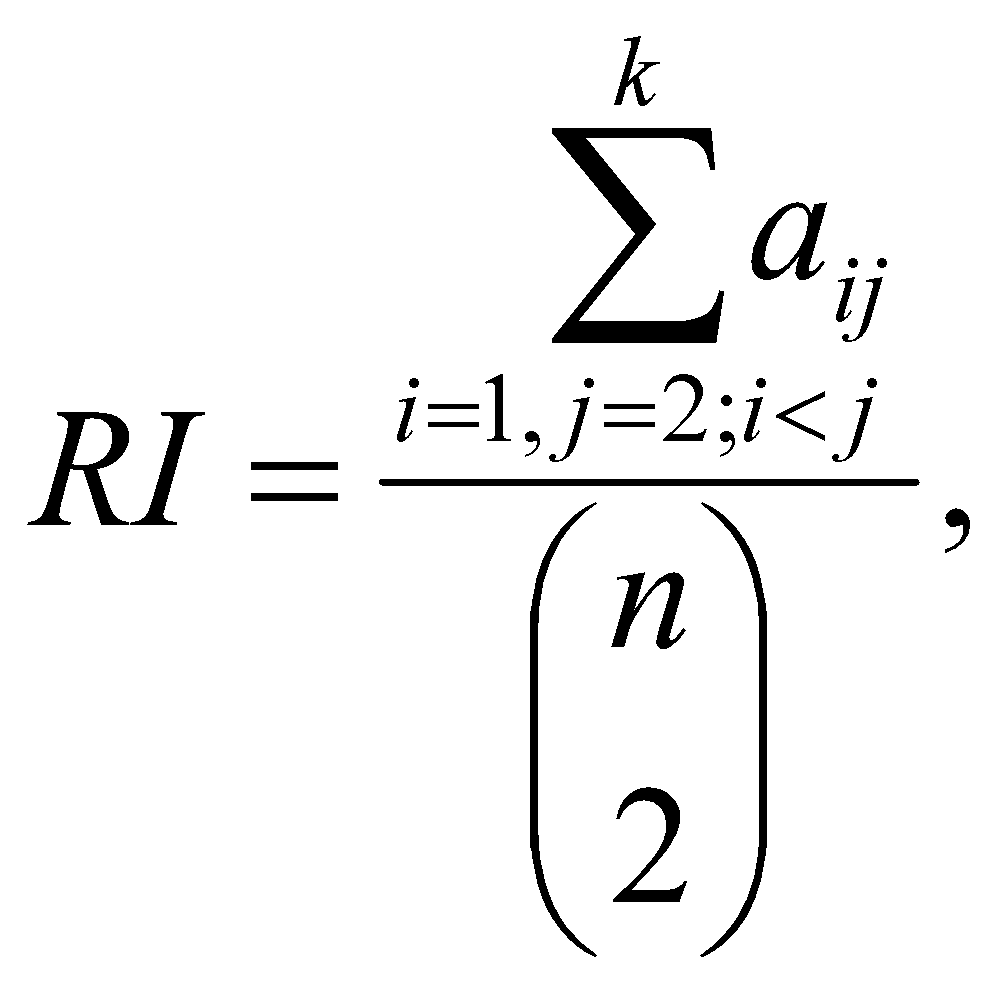
Downloads

Published

2024-09-30

Issue

Vol. 6 No. 2 (2024)

Section

Articles

License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Start from 2019 issues, authors who publish with JURNAL MOBILE AND FORENSICS agree to the following terms:

Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under a Creative Commons Attribution License (CC BY-SA 4.0) that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this journal.
Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial publication in this journal.
Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work.