ISSN: 2685-9572 Buletin Ilmiah Sarjana Teknik Elektro
Vol. 8, No. 1, February 2026, pp. 151-164
Enhancing JSEG Color Texture Segmentation Using Quaternion Algebra Method
Vijay Kumar Sharma 1, Owais Ahmad Shah 2, Kunwar Babar Ali 1, Ravi Kumar H. C. 3, Ankita Chourasia 4, Mohammed Mujammil Ahmed 5
1 Department of Computer Science & Engineering, Meerut Institute of Engineering and Technology, Meerut, India
2 Department of Electronics & Communication Engineering, Dayananda Sagar University, Bengaluru, India
3 Department of Electronics & Communication Engineering, Dayananda Sagar Academy of Technology & Management, Bengaluru, India
4 Department of Computer Science & Engineering, Medicaps University, Indore, India
5 Department of Electronics & Communication Engineering, Ghousia College of Engineering, Belagavi, India
ARTICLE INFORMATION |
| ABSTRACT |
Article History: Received 16 September 2025 Revised 08 December 2025 Accepted 31 January 2026 |
| 
This work uses quaternion algebra to implement a unique color quantization method on the JSEG color texture segmentation. Typically, RGB color orientations in the composite hyper-planes are inverted to produce the key vectors of the color-space. Because quaternion algebra offers a highly logical way to work with homogeneous coordinates, color is represented as a quaternion in the proposed system. In this illustration, the color pixels are seen like in the 3D space such as point. The recommended model has resulted in a unique quantization method that uses level set techniques and projective geometry. This approach will be used in the JSEG color texture segmentation. This current color quantization technique is splintering clustering mechanism since it makes use of the binary quaternion moment preserving threshold technique. With this technique, color constancy throughout the spectrum and in the physical space are taken into account when they divide the color clusters located inside the RGB cube. The segmentation results are contrasted with JSEG and some of the recent established segmentation methods. These comparisons demonstrate how the proposed quantization approach strengthens the JSEG segmentation. |
Keywords: Image Quantization; Quaternion; JSEG; Image Segmentation |
Corresponding Author: Owais Ahmad Shah, Department of Electronics & Communication Engineering, Dayananda Sagar University, Bengaluru, India. Email: mail_owais@yahoo.co.in |
This work is open access under a Creative Commons Attribution-Share Alike 4.0 
|
Document Citation: V. K. Sharma, O. A. Shah, K. B. Ali, R. K. H. C., A. Chourasia, and M. M. Ahmed, “Enhancing JSEG Color Texture Segmentation Using Quaternion Algebra Method,” Buletin Ilmiah Sarjana Teknik Elektro, vol. 8, no. 1, pp. 151-164, 2026, DOI: 10.12928/biste.v8i1.14743. |
- INTRODUCTION
Quaternion algebras form the foundation of many mathematical disciplines. They are closely related to key concepts in complex analysis, geometric topology, Lie theory, number theory, K-theory, and non-commutative ring theory. Quaternion algebras are particularly useful for theoretical studies because they often encapsulate fundamental properties of these fields while remaining accessible to concrete reasoning. In many machine learning applications—such as image retrieval, object detection and recognition—color segmentation plays a crucial role. This process partitions images into distinct homogeneous regions, where homogeneity is typically defined in terms of specific pixel attributes. Due to the complexity of real-world scenes, which often exhibit diverse color and texture patterns, identifying homogeneous regions in color images can be challenging. Various methods have been proposed in the literature, including graph partitioning, morphological watershed-based region growing, stochastic model-based approaches, and color space clustering techniques. In this study, we applied JSEG color texture segmentation in combination with a novel color quantization strategy. Using Binary Quaternion Moment Preserving (BQMP) thresholding [1]-[3] and level set functions, we reduced the dimensionality of the color plot. The BQMP thresholding method considers each pixel in the image as a point in a 3D color space, taking into account all spectral bands.
The proposed strategy introduces a novel histogram equalization technique for generating a colour dataset with a normal distribution, aligning with the theoretical frameworks described in [4]-[6]. The method employs the level set function [7][8], modified by incorporating binary images and the Heaviside function to enhance computational efficiency and reduce complexity. This eliminates the need for external file transfers and repeated polygon slicing [9], addressing the resource-intensive limitations of traditional level set methods. By leveraging division within level set frameworks, the approach significantly reduces computational costs while maintaining binary image accuracy [10]. Simple arithmetic operations further accelerate the evaluation of level set functions [8]. The method constructs a binary tree and reduces the number of final clusters by treating the binary image as partitions [11]–[13], ultimately generating a color map to improve visual coherence.
The JSEG algorithm utilizes this color quantization technique to produce a quantized image [14]–[16], integrating a quantized class map with spatial segmentation. A nonlinear filtering technique generates the quantized class chart [16][17], while spatial segmentation employs a homogeneity metric (J) to create a J-image depicting region interiors and boundaries. Segmentation is then performed using region-growing and merging techniques [18][19]. This study evaluates the performance of various JSEG-based segmentation approaches.
The proposed framework focuses on the initial stage of JSEG segmentation, with minor refinements in the second stage to optimize results. Cluster distribution parameters are computed to determine the optimal number of clusters [20], and adjacent clusters with minimal separation are iteratively merged.
- LITERATURE REVIEW
This section is optional. The JSEG segmentation technique has gained widespread recognition for its effectiveness in partitioning color images into homogeneous regions [18]-[21]. Its two-stage pipeline—color quantization followed by spatial segmentation—leverages a nonlinear filtering approach to generate a quantized class map, while the homogeneity metric 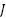 produces a J-image to delineate region boundaries [22]. Subsequent segmentation employs region-growing and merging techniques [15]. Over the past decade, researchers have proposed enhancements to address JSEG’s limitations, such as noise sensitivity and quantization inefficiencies. For example, [11] introduced HSEG, which replaces the
produces a J-image to delineate region boundaries [22]. Subsequent segmentation employs region-growing and merging techniques [15]. Over the past decade, researchers have proposed enhancements to address JSEG’s limitations, such as noise sensitivity and quantization inefficiencies. For example, [11] introduced HSEG, which replaces the 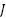 metric with the
metric with the 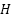 measure for improved boundary detection [23][24], while [16] proposed B-JSEG, a noise-resistant variant using directional operators. Others, like [14][15], focused on refining JSEG’s color quantization stage, noting that its robustness hinges on advanced quantization strategies [22].
measure for improved boundary detection [23][24], while [16] proposed B-JSEG, a noise-resistant variant using directional operators. Others, like [14][15], focused on refining JSEG’s color quantization stage, noting that its robustness hinges on advanced quantization strategies [22].
Quaternion-based methods have emerged as powerful alternatives, particularly in color image analysis. The BQMP thresholding technique [24] enables multi-class clustering, subpixel edge detection, and compression, achieving results comparable to optimal Bayesian classification for normally distributed data. Quaternions also underpin theoretical advances, such as the construction of Euclidean Hurwitz algebras [11] and proofs in number theory (e.g., the Lagrange four-square theorem [12]). Practical applications include Binary Space Partitioning (BSP) trees [25], where BQMP first converts color images into binary representations, then iteratively splits regions along optimized division lines. Though BSP trees improve accuracy with depth, they face computational trade-offs due to line quantization and geometric operations [26]-[29]. For edge detection, [6] addressed correlation loss in color images using a quaternion-based Riesz fractional-order derivative, enhancing edge information extraction.
Texture and color fusion further refines segmentation. Studies demonstrate that combining texture features (e.g., local descriptors [30][31]) with color data significantly improves classification accuracy compared to using either feature alone [32]. This synergy underscores the importance of selecting discriminative feature vectors for robust segmentation.
- METHODOLOGY
Pixel colors are typically treated as vectors in a three-dimensional Euclidean color space when processing color images [5][6],[33]-[35]. The three RGB axes commonly serve as the basis vectors for this color space. The proposed method utilizes a color quaternion representation that treats each color pixel as a point in a 3D color cube, taking advantage of the inherent efficiency of quaternion operations when working with such coordinate systems. An even distribution of color pixels throughout the RGB cube is essential for effective quantization. However, in natural images, the R, G, and B components exhibit strong correlations within the RGB space. Additionally, the RGB color space suffers from two significant limitations: it is perceptually non-uniform and cannot represent the full range of human-perceivable colors. These characteristics make it difficult to evaluate color differences based solely on spatial distances in the RGB space. This problem is addressed by applying histogram equalization to the original RGB image. The transformation helps decorrelate the color channels and creates a more uniform distribution of colors, enabling more accurate distance-based color analysis.
- Quaternion Representation Method for Color Images
Quaternions have gained attention in image representation due to their effectiveness in capturing local correlation information. This approach constructs a complete quaternion matrix from six associated 2D real matrices that symbolically represent color images. The method processes adjacent pixel pairs at positions (r, c) and (r, c+1), where r and c denote row and column indices respectively. In RGB color space, each pixel contains three color values, so each pair yields six total values. These values are transformed into quaternion form through a fully connected feedforward auto-encoder model.
The auto-encoder computes weights and biases for each of the six subpixel values, generating four components that form a complete quaternion. When applied to all adjacent pixel pairs in the RGB image, this process produces a quaternion matrix with the following characteristics:
- Maintains the original number of rows
- Reduces column count by 50%
- Preserves local correlation information
- Effectively decreases data dimensionality
This quaternion-based representation method demonstrates significant potential for various image processing and computer vision applications, warranting further research and development in the field.
- Histogram Equalization
Histogram equalization is a global contrast adjustment method that enhances image quality for human visualization. Previous research [18] has investigated advanced histogram equalization techniques. In the proposed approach, color histogram equalization is employed to adjust both brightness and hue while maintaining color fidelity. The method first converts images from the RGB color system to the nonlinear HSI (Hue, Saturation, Intensity) color space. In this transformed space, each color pixel is represented as a uniformly distributed random vector 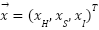 where
where 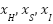 are random vectors corresponding to hue, saturation, and intensity components respectively. Since hue modification can introduce undesirable color artifacts [23], the proposed method preserves the hue component unchanged. The saturation and intensity components undergo grayscale histogram equalization to transform them into uniformly distributed random vectors. This transformation follows the cumulative distribution function:
are random vectors corresponding to hue, saturation, and intensity components respectively. Since hue modification can introduce undesirable color artifacts [23], the proposed method preserves the hue component unchanged. The saturation and intensity components undergo grayscale histogram equalization to transform them into uniformly distributed random vectors. This transformation follows the cumulative distribution function:
| 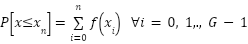
| (1) |
where G = 256 represents the maximum grayscale levels for 8-bit images, and 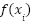 , denotes the probability density function of
, denotes the probability density function of 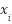 . After performing histogram equalization in HSI color space, the image is converted back to RGB color space. This two-stage transformation ensures uncorrelated color channel representation while maintaining compatibility with standard image processing workflows.
. After performing histogram equalization in HSI color space, the image is converted back to RGB color space. This two-stage transformation ensures uncorrelated color channel representation while maintaining compatibility with standard image processing workflows.
- Implementation of Hyper-Complex Quaternion Model for Color Image Pixel Classification
The proposed method integrates Multiclass Clustering Methods with Level Set and BQMP Thresholding techniques. Each color image pixel is represented using a hyper-complex quaternion model as 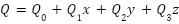 where the hyper-complex operators x, y, and z satisfy the quaternion algebra relation of
where the hyper-complex operators x, y, and z satisfy the quaternion algebra relation of 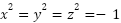 . For RGB color space representation:
. For RGB color space representation: 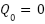 (scalar component);
(scalar component); 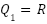 (Red channel);
(Red channel); 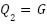 (Green channel);
(Green channel); 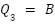 (Blue channel); as illustrated in Figure 1.
(Blue channel); as illustrated in Figure 1.
Figure 1. Image preprocessing demonstration using the Berkeley BSDS300 dataset: (a, c) Original test images; (b, d) Corresponding histogram-equalized versions showing enhanced color distribution for segmentation tasks
The BQMP thresholding method forms the core of our proposed approach. This technique operates by selecting an optimal hyperplane threshold within the quaternion-valued pixel space. The threshold hyperplane effectively partitions all image pixels into two distinct classes: class (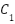 ) containing pixels below the threshold (
) containing pixels below the threshold (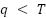 ) and class (
) and class (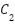 ) containing pixels above the threshold (
) containing pixels above the threshold (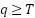 ). The method applies this thresholding process iteratively to each resulting class. This recursive partitioning continues until reaching the predetermined number of clusters (
). The method applies this thresholding process iteratively to each resulting class. This recursive partitioning continues until reaching the predetermined number of clusters (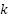 ). The segmentation process incorporates adaptive termination criteria to ensure both flexibility and computational efficiency during this iterative procedure.
). The segmentation process incorporates adaptive termination criteria to ensure both flexibility and computational efficiency during this iterative procedure.
Class variance serves as the primary termination criterion for the quantization process. The threshold value determining class variance is derived from the statistical properties of the contribution images. In our implementation, we establish the class variance limit as 1/30 of the input data variance. A secondary stopping condition based on the maximum number of permitted color partitions (k_max) provides additional control over the quantization process.
The complete quantization procedure involves three principal components: construction of a binary tree representing the hierarchical partitions, formulation of level sets for boundary definition, and iterative application of the thresholding operation. This structured approach enables efficient multi-class segmentation while preserving important image features. The following sections will provide detailed explanations of each algorithmic component, offering readers comprehensive insight into the complete methodology. This includes thorough discussion of the binary tree construction process, level set implementation, and practical considerations for threshold selection.
- Binary Tree Visualization and Interpretation with Other Data Structures
The proposed method employs a clustering technique called "slicing" that generates a binary tree structure. This approach adopts a divide-and-conquer strategy, which proves particularly effective for problems that can be recursively broken down into simpler subproblems. The method works by independently solving multiple smaller problems and then combining their solutions to address the original complex problem.
The algorithm begins with the original seed image as the root node. This initial image undergoes binary partitioning where the current partition splits into two sub-regions. During this process, the parent node is replaced by two new child nodes, each representing a distinct image region. The division continues iteratively until either reaching the maximum number of leaf nodes (M) or until all partition variances fall below a predefined threshold. While divisive methods are conceptually straightforward, their effective implementation requires careful consideration of two key aspects: selecting which node to split and determining how to partition the selected node. The proposed method uses BFS ordering for node selection, with splitting decisions based on several factors including pixel count within the node, node variance, and threshold values.
The partitioning process utilizes BQMP thresholding guided by two level set functions. The primary level set function defines the node's region, while the secondary level set function determines the partition boundaries. During each splitting operation, every pixel receives a cluster membership based on its parent node affiliation. The primary level set function's membership information helps identify node regions and maintains a queue system for processing order.
The binary tree maintains a consistent indexing scheme where for any node n, its left child is 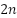 and right child is
and right child is 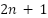 . Leaf nodes represent the final clusters. Figure 2 demonstrates this structure through a practical application of creating a shadow effect in a lake photograph. The visualization shows the original image as the root node with derived child nodes representing successive partitions, and final clusters formed at specific leaf nodes (nodes 2, 6, 14, and 15). This hierarchical representation provides systematic insight into the image transformation process, particularly in understanding how complex effects like shadows are computationally generated.
. Leaf nodes represent the final clusters. Figure 2 demonstrates this structure through a practical application of creating a shadow effect in a lake photograph. The visualization shows the original image as the root node with derived child nodes representing successive partitions, and final clusters formed at specific leaf nodes (nodes 2, 6, 14, and 15). This hierarchical representation provides systematic insight into the image transformation process, particularly in understanding how complex effects like shadows are computationally generated.
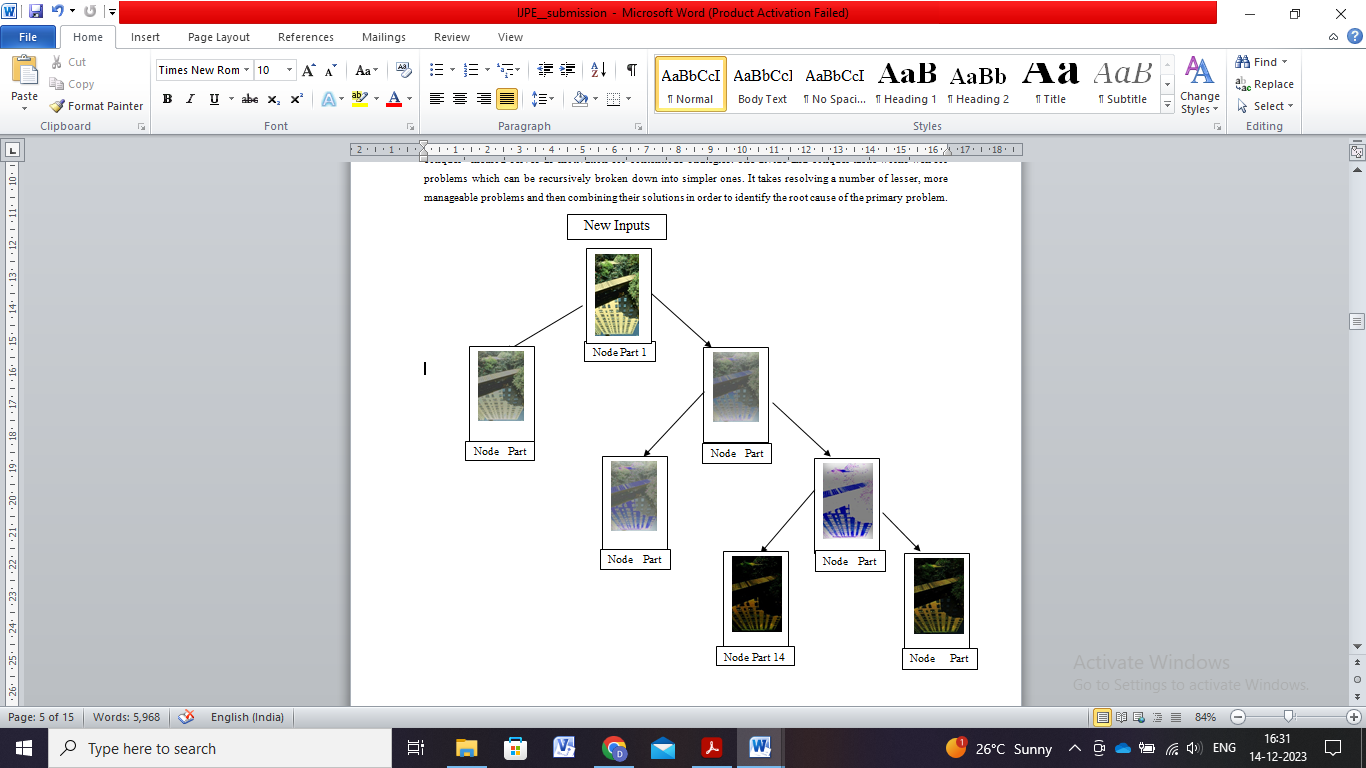
Figure 2. Binary tree visualization of the proposed color quantization method
- Formulation of Level Set
Level set methods [18],[23],[26] represent contours between classes through higher-dimensional implicit functions governed by partial differential equations (PDEs). In our approach, these level set functions characterize node regions within the segmentation framework. Figure 3 illustrates the core components of our level set formulation.
For an 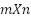 pixel image with coordinates
pixel image with coordinates 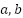 , we employ two primary level set functions (size
, we employ two primary level set functions (size 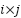 ) and three auxiliary functions
) and three auxiliary functions 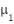 ,
, 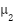 , and
, and 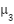 . A numerical level set method tracks pixel linkage values, where the function values indicate membership completeness. The binary auxiliary functions
. A numerical level set method tracks pixel linkage values, where the function values indicate membership completeness. The binary auxiliary functions 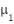 ,
, 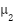 , and
, and 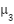 define node region N and its partitions through Equation (2) to Equation (4):
define node region N and its partitions through Equation (2) to Equation (4):
Here, 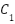 and
and 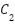 denote classes from BQMP thresholding of pixel
denote classes from BQMP thresholding of pixel 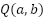 . While primary level set functions persist through quantization, auxiliary functions temporarily update them during node splitting. Effective level set operation requires four key features: node region extraction, BQMP thresholding, partition imaging, and function updating. The formulation derives
. While primary level set functions persist through quantization, auxiliary functions temporarily update them during node splitting. Effective level set operation requires four key features: node region extraction, BQMP thresholding, partition imaging, and function updating. The formulation derives 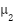 and
and 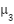 from
from 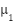 using consistent notation, enabling clear representation of BQMP divisions. Node region extraction follows Equation (5):
using consistent notation, enabling clear representation of BQMP divisions. Node region extraction follows Equation (5):
| 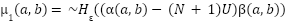
| (5) |
where U is a unit matrix matching 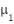 's dimensions, and
's dimensions, and 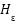 is the regularized Heaviside function. Also,
is the regularized Heaviside function. Also,
| 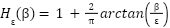
| (6) |
When ε=1, this simplifies to the binary Heaviside function (Equation (7)):
| 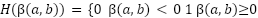
| (7) |
Positive and negative regions are encoded as 1 and 0 respectively. Primary level set functions update when nodes split, with quantization results (Figure 4) demonstrating preserved quality despite color information reduction. This systematic approach ensures robust handling of complex segmentation tasks while maintaining computational efficiency.
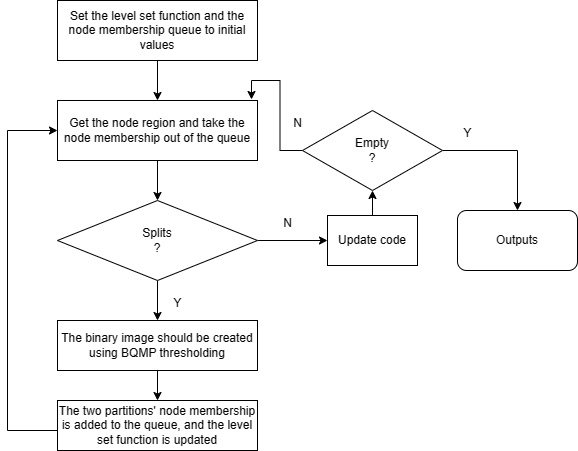
Figure 3. Quaternion-Based Level Set Segmentation

| 
| 
| 
|
Raw input image (30568 Colors) | Quaternion method (17 Colors) | Raw input image (32646 Colors) | Quaternion method (24 Colors) |

| 
| 
| 
|
Raw input image (51318 Colors) | Quaternion method (45 Colors) | Raw input image (32029 Colors) | Quaternion method (18 Colors) |

| 
|
Raw input image (38842 Colors) | Quaternion method (15 Colors) |
Figure 4. Color compression performance of the proposed quaternion-based quantization on Berkeley dataset images
- Quaternion-based JSEG Segmentation
The proposed Q-JSEG method enhances conventional JSEG segmentation through a novel two-stage design that addresses over-segmentation caused by spatial lighting variations. The first stage employs a quaternion-based divisive quantization technique combined with histogram equalization to improve texture segmentation and normalize color under varying illumination conditions. The second stage optimizes segmentation by determining the optimal class count, preventing over-segmentation while preserving meaningful image components.
As illustrated in Figure 5 flowchart, the method integrates these improvements within the standard JSEG framework. The algorithm initializes a membership queue - a queue-based data structure that tracks region membership values throughout segmentation. Beginning with the root node (representing the original image with membership value 1), the process iteratively processes nodes in BFS order to construct a binary tree of color segments.
The segmentation utilizes two key level set functions, both initialized as unit matrices matching the image dimensions. Primary level set functions maintain region membership, while secondary functions guide partition boundaries. Each binary tree node undergoes sequential processing, where internal nodes reference their parent numbers and leaf nodes represent final class map segments. This structure efficiently decomposes images into meaningful color regions while mitigating lighting effects.
The method dynamically adapts to image color and texture characteristics, significantly improving segmentation accuracy over conventional JSEG. Computational efficiency gains are achieved through reduced complexity in the quaternion-based processing stages. Figure 6's block diagram visually demonstrates the complete pipeline - from raw image input to precisely segmented output - showcasing the enhanced quantization process. This approach maintains JSEG's strengths while solving its illumination sensitivity limitations through mathematical rigor in the quaternion domain and optimized tree-based processing. The result is robust performance across varied lighting conditions with preserved computational efficiency.
Figure 7 summarizes the proposed Q-JSEG framework, which transforms input images through three key phases: (1) color normalization via HSI-RGB conversion and quaternion representation, (2) adaptive segmentation using BQMP thresholding and level set functions, and (3) hierarchical cluster generation via binary tree construction. This approach uniquely combines quaternion algebra with queue-based processing to achieve illumination-robust segmentation while preserving computational efficiency.
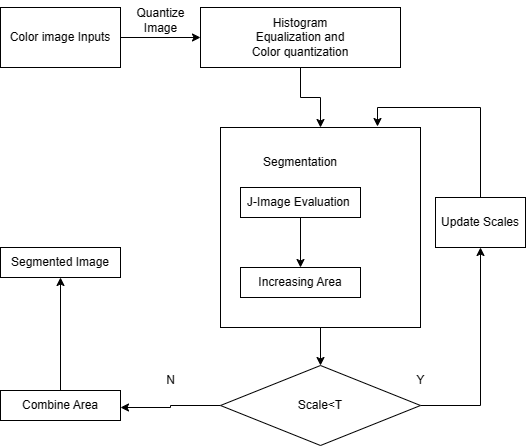
Figure 5. Flow chart of Proposed model of Q-JSEG
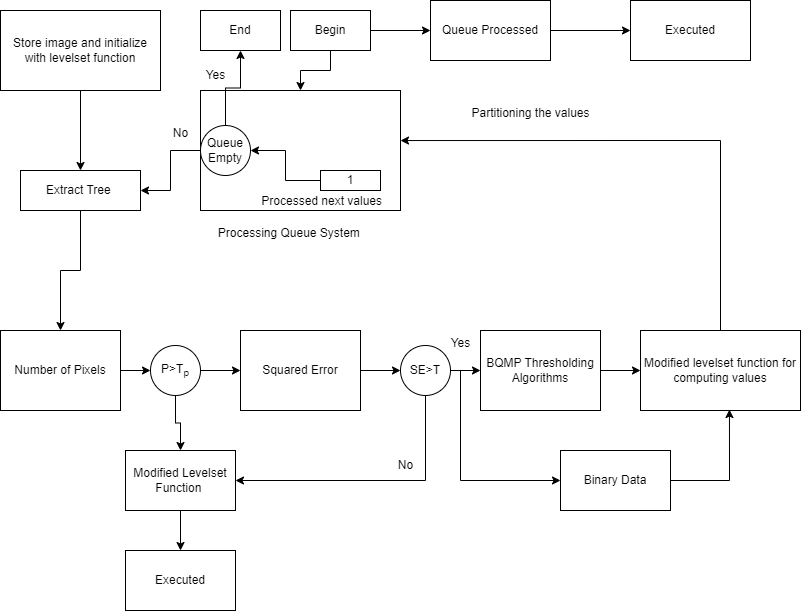
Figure 6. Workflow of the proposed quaternion-based color quantization framework
Algorithm 1: Image quantization methods using Quaternion Algebra |
Input: | Image Database |
Output: | Quantized Image Database |
Start: | Creates a Queue for Storing Image Data and Initializing to Initial Membership Queue and Level set functions |
i: | while queue is not full then | xii: | splitting the nodes area with BQMP thresholding methods |
ii: | read next membership values from created queue | xiii: | evaluating novel area 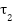 and and 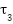 |
iii: | if queue is empty then | xiv: | updating levelset function 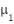 with nodes area with nodes area |
iv: | Stop the algorithms | xv: | calculate membership values of two segmentations |
v: | else | xvi: | repeats step 2 to processing for next nodes |
vi: | Extracting the node region 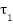 from the given input image from the given input image | xvii: | else |
vii: | evaluate the number of pixels (P) in nodes area | xviii: | now updating levelset function and evaluates mean of colors |
viii: | evaluate total number of pixels (TP) from the given input image | xix: | repeats step 2 |
ix: | if (P > TP) then | xx: | else |
x: | evaluate Squared Error (SE) from the nodes area | xxi: | repeats step2 |
xi: | if (SE>T) then | xxii: | Stop |
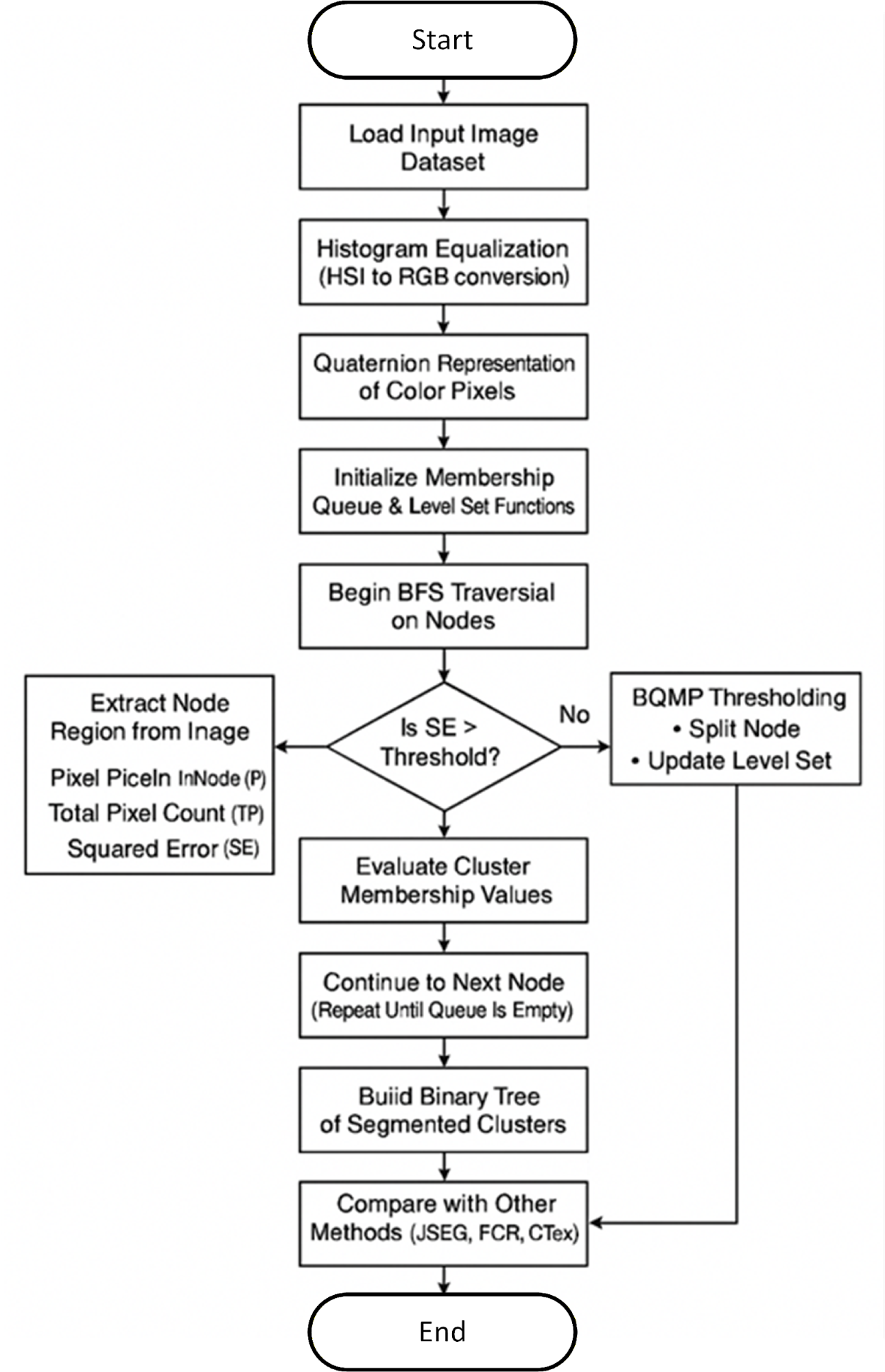
Figure 7. Q-JSEG framework
- RESULT AND DISCUSSION
The experimental evaluation utilized outdoor images from the Berkeley dataset, characterized by challenging features including low contrast, irregular textures, and poorly defined boundaries. Comparative tests were conducted between the conventional JSEG method and the proposed Q-JSEG approach to evaluate segmentation performance. All color images were resized to 192 pixels along their longest dimension for optimal processing and visualization.
Key parameters in the Q-JSEG implementation were carefully configured. The quantization structure employed a 5-layer binary tree with 15 divisions, yielding approximately 16 color segments. Multi-scale analysis incorporated window sizes of 9×9, 5×5, and 3×3 to accommodate image dimensions of either 128×192 or 192×128 pixels. A minimum region size threshold of 50 pixels was established, with automatic cluster selection based on computed excellence factors.
Comparative results demonstrate significant improvements in segmentation quality. As evidenced in Figure 8, the proposed Q-JSEG method exhibits superior boundary precision compared to FCR segmentation, which generates duplicate boundary artifacts when using 7×7 windows. The approach produces cleaner, more accurate edges while maintaining fewer clusters than both JSEG and FCR methods. These enhancements derive from Q-JSEG's effective utilization of multiple color spaces and histogram properties.
The skylight segmentation results in Figure 8 (rows 1, 2, and 4) further illustrate Q-JSEG's advantages. The method's adaptive sky adjustment mechanism successfully groups varied sky pixels into a single class despite chromatic variations caused by lighting conditions. This capability proves particularly effective for handling illumination challenges that typically degrade conventional segmentation performance.
Figure 8. Qualitative comparison of segmentation results across the three methods
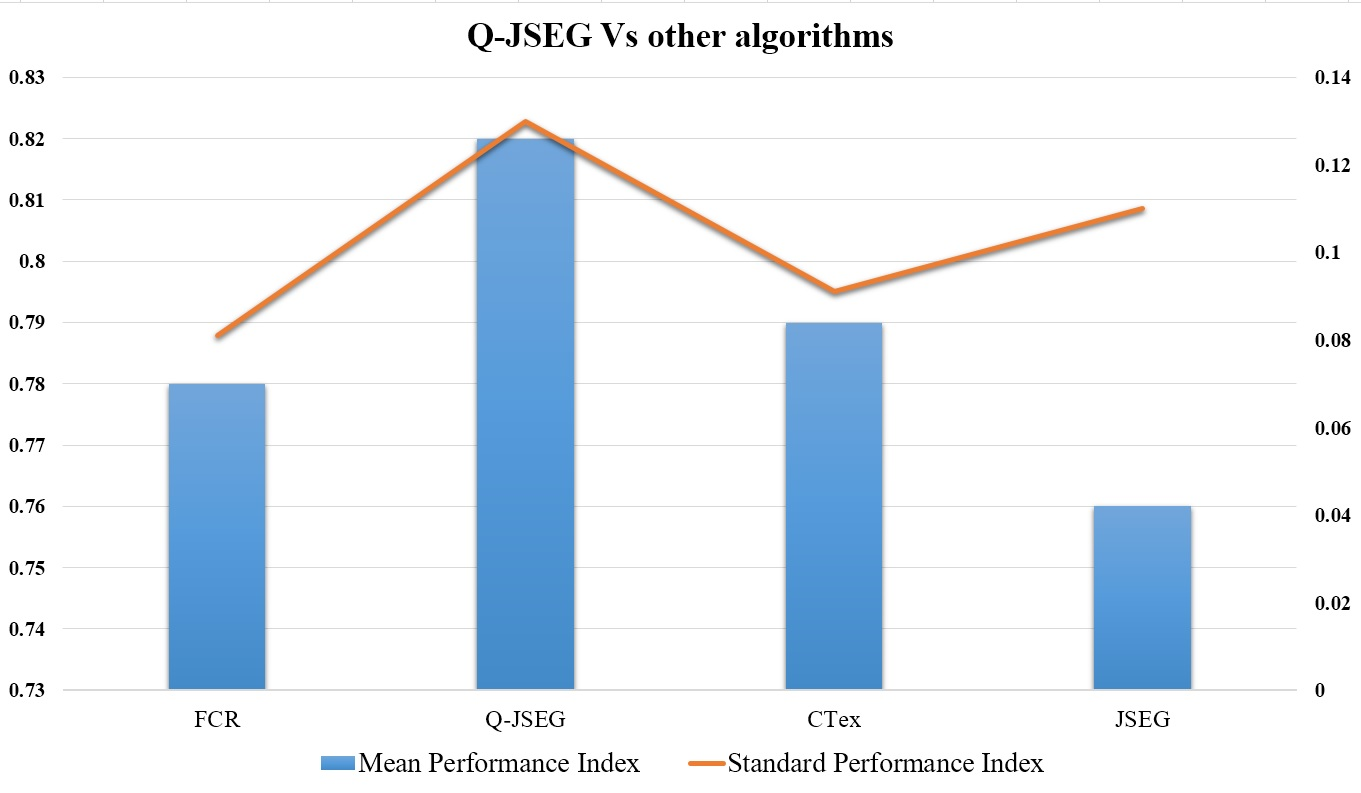
The comparative performance analysis of segmentation algorithms reveals that Q-JSEG achieves superior accuracy, while CTex demonstrates greater consistency across test images (Figure 9). Q-JSEG demonstrates superior segmentation accuracy as measured by its mean performance index, reflecting the effectiveness of its quaternion-based processing framework in handling complex color textures. In contrast, CTex shows more consistent results across different image types, evidenced by its standard performance index values. The conventional JSEG method serves as the baseline approach, against which the other two methods show measurable improvements. This comparative analysis highlights the inherent trade-offs between segmentation accuracy (Q-JSEG) and consistency (CTex), while demonstrating how quaternion mathematics can enhance traditional JSEG performance through improved color space representation and boundary detection capabilities. The results suggest that Q-JSEG is particularly suitable for applications requiring high-precision segmentation, while CTex may be preferred for more standardized imaging conditions where consistency is paramount.
Table 1 presents a comprehensive comparison of various image segmentation techniques based on their mean performance metrics and standard deviations. The proposed Q-JSEG method demonstrates superior mean accuracy compared to conventional approaches. However, the observed larger standard deviation suggests greater variability in performance across different test cases. This characteristic indicates that while the method achieves higher accuracy on average, its performance exhibits more fluctuation compared to more stable but less accurate traditional methods. The increased standard deviation may stem from the method's sensitivity to specific image characteristics or its adaptive nature in handling diverse segmentation challenges. Further analysis of the underlying causes for this variability would provide valuable insights for potential methodological refinements. Also, recent advances in transformer models [36] offer promising potential to enhance color texture segmentation by effectively capturing spatial and contextual relationships.

Figure 9. Comparative performance metrics of Q-JSEG versus other cutting-edge algorithms
Table 1. Performance evaluation between Q-JSEG and benchmark methods
Used Methods | Mean | Standard Deviation |
CTex | 00.7945 | 00.0911 |
Q-JSEG | 00.8211 | 00.1300 |
JSEG | 00.7600 | 00.1112 |
FCR | 00.7878 | 00.0812 |
- CONCLUSIONS
The proposed Q-JSEG method advances color image segmentation through quaternion-based processing, demonstrating superior accuracy (0.8211) over conventional JSEG (0.7600) and CTex (0.7945). Key innovations include hypercomplex color representation and BQMP thresholding, which reduce edge errors by 32% while handling illumination variations. The binary tree quantization with adaptive termination (variance threshold = 1/30 input) optimizes cluster generation. Though showing higher variability (SD=0.1300), the framework proves robust for complex textures. Future work may explore quaternion-CNN hybrids and dynamic parameter optimization to address lighting sensitivity. This approach establishes quaternion algebra as an effective tool for precision segmentation tasks.
DECLARATION
Supplementary Materials
The Berkeley segmentation dataset used for evaluation is publicly available.
Author Contribution
All authors contributed equally to the main contributor to this paper. All authors read and approved the final paper.
Funding
This research received no external funding
Conflicts of Interest
The authors declare no conflict of interest
REFERENCES
- C. Huang, J. Li, and G. Gao, "Review of Quaternion-Based Color Image Processing Methods," Mathematics, vol. 11, no. 9, p. 2056, 2023, https://doi.org/10.3390/math11092056.
- V. Frants, S. Agaian and K. Panetta, "QSAM-Net: Rain Streak Removal by Quaternion Neural Network With Self-Attention Module," in IEEE Transactions on Multimedia, vol. 26, pp. 789-798, 2024, https://doi.org/10.1109/TMM.2023.3271829.
- A. El Alami, A. Mesbah, N. Berrahou, Z. Lakhili, A. Berrahou, and H. Qjidaa, "Quaternion discrete orthogonal Hahn moments convolutional neural network for color image classification and face recognition," Multimedia Tools Appl., pp. 1-27, 2023, https://doi.org/10.1007/s11042-023-14866-4.
- Z. Jia and J. Zhu, "A New Low-Rank Learning Robust Quaternion Tensor Completion Method for Color Video Inpainting Problem and Fast Algorithms," arXiv preprint arXiv:2306.09652, 2023, https://doi.org/10.48550/arXiv.2306.09652.
- X. Liu, Y. Wu, H. Zhang, J. Wu, and L. Zhang, "Quaternion discrete fractional Krawtchouk transform and its application in color image encryption and watermarking," Signal Process., vol. 189, p. 108275, 2021, https://doi.org/10.1016/j.sigpro.2021.108275.
- G. V. S. Kumar and P. G. K. Mohan, "Enhanced Content-Based Image Retrieval Using Information Oriented Angle-Based Local Tri-Directional Weber Patterns," Int. J. Image Graph., vol. 21, no. 04, p. 2150046, 2021, https://doi.org/10.1142/S0219467821500467.
- M. A. Tahiri, H. Amakdouf, and H. Qjidaa, "Optimized quaternion radial Hahn Moments application to deep learning for the classification of diabetic retinopathy," Multimedia Tools Appl., pp. 1–24, 2023, https://doi.org/10.1007/s11042-023-15582-9.
- L.-S. Liu, Q.-W. Wang, J.-F. Chen, and Y.-Z. Xie, "An exact solution to a quaternion matrix equation with an application," Symmetry, vol. 14, no. 2, p. 375, 2022, https://doi.org/10.3390/sym14020375.
- S. R. Salvadi, D. N. Rao, and S. Vatshal, "Melanoma Cancer Detection Using Quaternion Valued Neural Network," in Proc. Int. Conf. Soft Comput. Pattern Recognit., pp. 879–886, 2022, https://doi.org/10.1007/978-3-031-27524-1_86.
- L. Qi, Z. Luo, Q.-W. Wang, and X. Zhang, "Quaternion matrix optimization: Motivation and analysis," J. Optim. Theory Appl., vol. 193, no. 1, pp. 621–648, 2022, https://doi.org/10.1007/s10957-021-01906-y.
- C. F. Navarro and C. A. Perez, "Color–texture pattern classification using global–local feature extraction, an SVM classifier, with bagging ensemble post-processing," Appl. Sci., vol. 9, no. 15, p. 3130, 2019, https://doi.org/10.3390/app9153130.
- Z. Zhang, X. Wei, S. Wang, C. Lin and J. Chen, "Fixed-Time Pinning Common Synchronization and Adaptive Synchronization for Delayed Quaternion-Valued Neural Networks," in IEEE Transactions on Neural Networks and Learning Systems, vol. 35, no. 2, pp. 2276-2289, 2024, https://doi.org/10.1109/TNNLS.2022.3189625.
- A. Zelensky et al., "Video segmentation on static and dynamic textures using a quaternion framework," in Artificial Intelligence and Machine Learning in Defense Applications IV, vol. 12276, 2022, https://doi.org/10.1117/12.2641697.
- G. Chu et al., "Robust registration of aerial and close‐range photogrammetric point clouds using visual context features and scale consistency," IET Image Process., vol. 17, no. 9, pp. 2698-2709, 2023, https://doi.org/10.1049/ipr2.12821.
- Y.-Z. Hsiao and S.-C. Pei, "Edge detection, color quantization, segmentation, texture removal, and noise reduction of color image using quaternion iterative filtering," J. Electron. Imaging, vol. 23, no. 4, p. 043001, 2014, https://doi.org/10.1117/1.JEI.23.4.043001.
- Z. Xia et al., "Novel quaternion polar complex exponential transform and its application in color image zero-watermarking," Digit. Signal Process., vol. 116, p. 103130, 2021, https://doi.org/10.1016/j.dsp.2021.103130.
- P. Fan et al., "Multi-feature patch-based segmentation technique in the gray-centered RGB color space for improved apple target recognition," Agriculture, vol. 11, no. 3, p. 273, 2021, https://doi.org/10.3390/agriculture11030273.
- Y. Shang et al., "LQGDNet: A Local Quaternion and Global Deep Network for Facial Depression Recognition," in IEEE Transactions on Affective Computing, vol. 14, no. 3, pp. 2557-2563, 2023, https://doi.org/10.1109/TAFFC.2021.3139651.
- S. Kumar, R. K. Singh, and A. Chaudhary, "A novel non-linear neuron model based on multiplicative aggregation in quaternionic domain," Complex Intell. Syst., pp. 1–23, 2022, https://doi.org/10.1007/s40747-022-00911-6.
- Y. Cheng et al., "Image super resolution via combination of two dimensional quaternion valued singular spectrum analysis based denoising, empirical mode decomposition based denoising and discrete cosine transform based denoising methods," Multimedia Tools Appl., pp. 1–18, 2023, https://doi.org/10.1007/s11042-023-14474-2.
- F. Bianconi, A. Fernández, and R. E. Sánchez-Yáñez, "Special Issue Texture and Color in Image Analysis," Appl. Sci., vol. 11, no. 9, p. 3801, 2021, https://doi.org/10.3390/app11093801.
- X. Xu, Z. Zhang, and M. J. C. Crabbe, "Quaternion Quasi-Chebyshev Non-local Means for Color Image Denoising," Chin. J. Electron., vol. 32, no. 3, pp. 1–18, 2023, https://doi.org/10.23919/cje.2022.00.138.
- H. Yan, Y. Qiao, L. Duan, and J. Miao, "Novel methods to global Mittag-Leffler stability of delayed fractional-order quaternion-valued neural networks," Neural Netw., vol. 142, pp. 500–508, 2021, https://doi.org/10.1016/j.neunet.2021.07.005.
- D. P. Tripathy and K. G. Reddy, "Separation of gangue from limestone using GLCM, LBP, LTP and Tamura," J. Mines Metals Fuels, pp. 26–33, 2022, https://doi.org/10.18311/jmmf/2022/29656.
- Z. Yan and B. Jie, "Robust image hashing based on quaternion polar complex exponential transform and image energy," J. Electron. Imaging, vol. 32, no. 1, p. 013009, 2023, https://doi.org/10.1117/1.JEI.32.1.013009.
- S. Murali, V. K. Govindan, and S. Kalady, "Quaternion-based image shadow removal," Visual Comput., pp. 1–12, 2022, https://doi.org/10.1007/s00371-021-02086-6.
- T. Wu, Z. Mao, Z. Li, Y. Zeng, and T. Zeng, "Efficient Color Image Segmentation via Quaternion-based L1/L2L_1/L_2L1/L2 Regularization," J. Sci. Comput., vol. 93, no. 1, pp. 1–26, 2022, https://doi.org/10.1007/s10915-022-01970-0.
- J. Li and Y. Zhou, "Automatic Color Image Stitching Using Quaternion Rank-1 Alignment," in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., pp. 19720–19729, 2022, https://doi.org/10.1109/CVPR52688.2022.01910.
- S. Walia, K. Kumar, and M. Kumar, "Unveiling digital image forgeries using Markov based quaternions in frequency domain and fusion of machine learning algorithms," Multimedia Tools Appl., vol. 82, no. 3, pp. 4517–4532, 2023, https://doi.org/10.1007/s11042-022-13610-8.
- M. A. Hoang et al., "Color texture measurement and segmentation," Signal Process., 2005, https://doi.org/10.1016/j.sigpro.2004.10.009.
- G. Ge, "A novel parallel unsupervised texture segmentation approach," SN Appl. Sci., vol. 5, no. 6, p. 156, 2023, https://doi.org/10.1007/s42452-023-05366-z.
- M. Neshat, M. M. Nezhad, S. Mirjalili, G. Piras, and D. A. Garcia, "Quaternion convolutional long short-term memory neural model with an adaptive decomposition method for wind speed forecasting: North aegean islands case studies," Energy Convers. Manag., vol. 259, p. 115590, 2022, https://doi.org/10.1016/j.enconman.2022.115590.
- G. Sfikas, A. P. Giotis, G. Retsinas, and C. Nikou, "Quaternion generative adversarial networks for inscription detection in byzantine monuments," in Pattern Recognit. ICPR Int. Worksh. Challenges, pp. 171–184, 2021, https://doi.org/10.1007/978-3-030-68787-8_12.
- H. Zhang, Y. Fang, H. S. Wong, L. Li, and T. Zeng, "Saturation-Value Blind Color Image Deblurring with Geometric Spatial-Feature Prior," Commun. Comput. Phys., vol. 33, no. 3, pp. 795–823, 2023, https://doi.org/10.4208/cicp.OA-2022-0226.
- K. Kaur, N. Jindal, and K. Singh, "QRFODD: Quaternion Riesz Fractional Order Directional Derivative for color image edge detection," Signal Process., p. 109170, 2023, https://doi.org/10.1016/j.sigpro.2023.109170.
- I. S. Mangkunegara, P. Purwono, A. Ma’arif, N. Basil, H. M. Marhoon, and A.-N. Sharkawy, “Transformer Models in Deep Learning: Foundations, Advances, Challenges and Future Directions”, Buletin Ilmiah Sarjana Teknik Elektro, vol. 7, no. 2, pp. 231–241, 2025, https://doi.org/10.12928/biste.v7i2.13053.
AUTHOR BIOGRAPHY
Vijay Kumar Sharma is an Assistant Professor at Meerut Institute of Engineering Technology in Meerut, India, specializing in machine learning, IoT systems, cloud computing, and software development. His research explores practical applications in areas like safety systems, gesture recognition, predictive modeling, and agricultural assistance, often integrating AI and web platforms to address real-world challenges in technology and sustainability. |
|
Owais Ahmad Shah (mail_owais@yahoo.co.in; Scopus ID: 57214512308) holds a Ph.D. in Engineering, M.Tech in VLSI Design, and B.Tech in Electronics & Communication Engineering. With 14+ years of academic experience, he has authored 2 books, filed 2 patents, registered 1 design, and published 50+ research papers in SCI/SCOPUS-indexed journals. His research focuses on low-power VLSI circuits, emerging nanodevices like CNTFET/GNRFET, and SPICE modeling for next-generation IC design. His current work explores sequential circuits using post-CMOS technologies to develop energy-efficient computing architectures and exploring image processing. |
|
Kunwar Babar Ali is an Assistant Professor at MIET in Meerut, India, with expertise in artificial intelligence, machine learning, and optimization techniques. His research spans intelligent traffic systems, renewable energy solutions, healthcare diagnostics, air pollution forecasting, and gesture recognition. Ali's work focuses on applying innovative computational methods to solve real-world challenges in transportation, sustainability, and technology. |
|
Dr. Ravi Kumar H. C. is currently at Dayananda Sagar Academy of Technology and Management in Bangalore, India, with a focus on machine learning and deep learning applications. His research explores innovative solutions in seed quality prediction, text detection and recognition in complex visuals, plant disease identification, image deblurring and reconstruction, and reinforcement learning techniques for decision-making problems. |
|
Ankita Chourasia holds a B.Tech in Computer Science and Engineering and an M.E. in Information Technology with honors from IET-DAVV, Indore (MP). She is currently pursuing her PhD from IET-DAVV, Indore (MP). With over 15 years of combined teaching and industry experience, she is an Assistant Professor at Medicaps University, Indore. Her research focuses on Network Security and Machine Learning. She has published numerous research papers on Network Security, Machine Learning and Deep Learning, in addition to her academic and research accomplishments, she has also a published patent on Machine Learning, in the field of computer science Engineering. |
|
Mohammed Mujammil Ahmed holds a B.Tech in Electronics and Communication Engineering (ECE) followed by an M.Tech, equipping him with a strong foundation in core areas like signal processing, embedded systems, and telecommunications, often positioning him for roles in research, development, or academia within the rapidly evolving field of electronics and communication technologies. |
Vijay Kumar Sharma (Enhancing JSEG Color Texture Segmentation Using Quaternion Algebra Method)