ISSN: 2685-9572 Buletin Ilmiah Sarjana Teknik Elektro
Vol. 7, No. 4, December 2025, pp. 907-917
Power System Stabilizer Optimization Based on Modified Black‑Winged Kite Algorithm
Widi Aribowo 1, Laith Abualigah 2, Diego Oliva 3, Nur Vidia Laksmi B 1, Fithrotul Irda Amaliah 1,
As’ad Shidqy Aziz 1, Hewa Majeed Zangana 4
1 Department of Electrical Engineering, Faculty of Vocational Studies, Universitas Negeri Surabaya, Surabaya, Indonesia
2 Computer Science Department, Al al-Bayt University, Mafraq 25113, Jordan
3 Depto. de Ingeniería Electro-Fotónica, Universidad de Guadalajara, CUCEI, Guadalajara, México
4 IT Department, Duhok Technical College, Duhok Polytechnic University, Duhok, Iraq
ARTICLE INFORMATION |
| ABSTRACT |
Article History: Received 07 September 2025 Revised 22 November 2025 Accepted 28 November 2025 |
| 
This article presents a Modified Method for tuning the parameters of a power system stabilizer (PSS). This article suggests a different approach that modifies the Black Kite Algorithm (BKA). The Black Kite (BKA) method is inspired by the migratory and predatory habits of the black kite. BKA combines the Leader and Cauchy mutation strategies to improve the algorithm's capacity for global search and convergence rate. This article includes comparative simulations of the PSS objective function and transient response to verify the effectiveness of the suggested strategy. The study validates the proposed method through comparison with both conventional techniques and the original BKA. Simulation results demonstrate that, when benchmarked against competing algorithms, the proposed method consistently yields optimal performance and exhibits faster convergence in certain scenarios. Notably, it reduces undershoot and overshoot by an average of 65% and 90.22%, respectively, compared to the PSS-Lead Lag method. Furthermore, the proposed approach not only minimizes overshoot and undershoot but also achieves a significantly faster settling time. |
Keywords: Black‑Winged Kite Algorithm; Metahueristic; Power System Stabilizer; Power System Stability; Artificial Intelligence |
Corresponding Author: Widi Aribowo, Department of Electrical Engineering, Faculty of Vocational, Universitas Negeri Surabaya, Surabaya, Indonesia. Email: widiaribowo@unesa.ac.id |
This work is open access under a Creative Commons Attribution-Share Alike 4.0 
|
Document Citation: W. Aribowo, L. Abualigah, D. Oliva, N. V. L. B, F. I. Amaliah, A. S. Aziz, and H. M. Zangana, “Power System Stabilizer Optimization Based on Modified Black‑Winged Kite Algorithm,” Buletin Ilmiah Sarjana Teknik Elektro, vol. 7, no. 4, pp. 907-917, 2025, DOI: 10.12928/biste.v7i4.14669. |
INTRODUCTION
In today’s modern power systems characterized by ever-increasing load demands, highly interconnected architectures, and geographically dispersed network topologies maintaining system stability has become a critical challenge [1]-[4]. Ensuring the reliable and uninterrupted delivery of electricity requires not only continuous generation and efficient distribution but also strict adherence to operational constraints that keep key system parameters such as frequency and voltage within acceptable limits [5]. This stability is fundamentally contingent upon the precise real-time balance between power generation and load demand. However, load profiles are inherently dynamic, often exhibiting significant unpredictability and temporal variability. Such fluctuations cause the power system to operate across a wide range of operating points, which in turn leads to deviations in scheduled power exchanges and frequency excursions [6]-[8].
These disturbances can propagate through the network, potentially triggering cascading effects that compromise overall system reliability. If not adequately mitigated, such phenomena may result in reduced damping of electromechanical oscillations, voltage instability, or even partial or widespread blackouts thereby exacerbating system instability [9]-[11]. Consequently, advanced control strategies and real-time monitoring mechanisms are indispensable for preserving the dynamic and transient stability of modern power grids [12]-[14]. The ability of an electric power system to function steadily in the face of disruptions or changes in its operational environment is known as power system stability [15]-[18]. When the power system's stability is compromised, other disruptions may follow, which could lead to blackouts or widespread power outages [19] [20]. Therefore, power system operators, electrical engineers, and researchers in the power business need to have a solid understanding of power system stability and how to manage it [21]. To guarantee ideal power system stability, methods include steady state stability analysis, transient stability analysis, and the use of complex control algorithms are used [22].
A device called a Power System Stabilizer (PSS) is used in electric power systems to improve the system's dynamic stability [23]. Electric generators typically have PSS installed, which regulates the generator field strengthening (excitation) to offset disturbances and preserve voltage and frequency stability in the system [24]-[26]. When it comes to handling extremely complicated power systems or systems with a lot of variable variation, conventional PSS is not successful enough. Conventional PSS can experience delays in response to disturbances due to slow or suboptimal settings [27]. Improper tuning can reduce PSS performance or even cause system destabilization if its control signals are not set correctly [28].
Using AI techniques in PSS can enhance power systems' overall performance, responsiveness, and dependability. Artificial Intelligence (AI) is a branch of computer science that aims to create a system or machine that is able to mimic human cognitive abilities [29], such as learning, understanding language, recognizing patterns, making decisions, and solving problems [30]-[33]. Numerous academics have introduced AI techniques, particularly metaheuristic approaches in PSS, like the Archimedes optimization algorithm [34], gradient-based optimizers [35], sand cat swarm optimization [36], and Gray Wolf Optimizer [37]. Even though several academics have offered AI methods to PSS, there is always room for more investigation into PSS and AI intersections.
In this article we present a PSS tuning approach using a modified Black‑winged kite algorithm. Black Kite Algorithm (BKA), a meta-heuristic optimization algorithm inspired by the migratory and predatory behavior of black kites [38]. BKA can get stuck at local optima, especially if the parameters are not well-tuned or the initial population is not diverse enough. The final solution may not be the best global solution, especially for highly non-linear or multi-modal objective functions. This research has contributions, namely:
- A modification method for the black-winged kite algorithm called MBKA is presented. The modification is done by adding equations that can expand the exploration and exploitation capabilities. The convergence value will be observed by looking at the lowest value which is the best.
- Application of MBKA to PSS in single machine
- Assess the ability of MBKA-based controllers to improve PSS performance in single machine.
- Compare the MBKA applied to PSS with conventional methods as lead-lag, and the original BKA in single machine
The article consists of the method, mathematical formulation, and explanation of the proposed method approach along with its pseudocode in section 2. Section 3 is a simulation and discussion. The final section contains the research conclusions.
METHODS
Black‑Winged Kite Algorithm
BKA is a straightforward and successful metaheuristic optimization technique. Black-winged kite migration behavior and attack strategy serve as the basis for BKA, which is based on these stages of migration and attack. In BKA, population initialization begins with the creation of a random solution set, as is typical of other metaheuristic techniques.
Where 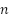 is the number of populations,
is the number of populations, 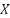 is the sorted population matrix, and
is the sorted population matrix, and 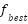 is the vector of the objective function values.
is the vector of the objective function values. 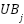 and
and 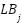 are the upper and lower bounds. The Black-winged kite population's ideal location is thought to be reached when the BKA, during the initialization phase, chooses the individual with the highest fitness value as the
are the upper and lower bounds. The Black-winged kite population's ideal location is thought to be reached when the BKA, during the initialization phase, chooses the individual with the highest fitness value as the 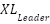 in the initial population.
in the initial population.
Assaultive Conduct
Black-winged kites are predators on tiny grassland mammals and insects. During a fight, they adapt the angles of their wings and tails to the speed of the wind, hover silently to study their prey, and then swiftly plunge and attack. Several assault behaviors are included in this technique for global search and exploration. Black-winged kite racing at breakneck speed in the direction of its prey. A mathematical model of black-winged kite attack behavior is as follows:
| 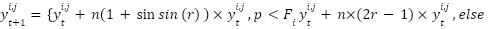
| (4) |
| 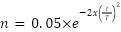
| (5) |
Where 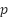 is a constant value of 0.9 and
is a constant value of 0.9 and 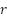 is a random number between 0 and 1.
is a random number between 0 and 1. 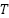 represents both the total number of iterations and the number of iterations that have been finished up to this point.
represents both the total number of iterations and the number of iterations that have been finished up to this point.
Migration Behavior
The leader will resign from his position as leader and join the migrating population if the current population's fitness value is less than the random population value, suggesting that it is unfit to lead the population in the future. In contrast, the population will be led until it achieves its objective if the fitness value of the current population is higher than that of a random population. This tactic might choose exceptional leaders on the fly to guarantee the success of migration.
| 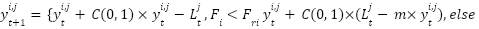
| (6) |
| 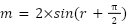
| (7) |
Thus far in the 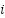 th iteration,
th iteration, 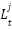 stands for the top scorer of the Black-winged kites in the
stands for the top scorer of the Black-winged kites in the 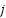 th dimension. Here,
th dimension. Here, 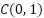 is the Cauchy mutation. A continuous probability distribution with two parameters is called a one-dimensional Cauchy distribution. The probability density function of the one-dimensional Cauchy distribution is represented by the following equation:
is the Cauchy mutation. A continuous probability distribution with two parameters is called a one-dimensional Cauchy distribution. The probability density function of the one-dimensional Cauchy distribution is represented by the following equation:
| 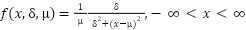
| (8) |
Its probability density function will take on the conventional form for δ=1, μ=0. The exact formula is as follows:
| 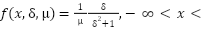
| () |
Power System Stabilizers
Using additional stabilizing signals to control the field excitation of the generator rotor is the fundamental function of PSS, which helps to dampen oscillations in the rotor [39][40]. The PSS generates an electrical torque component in step with the rotor speed deviation in order to provide adequate damping. In the excitation system, PSS will lessen generator rotor oscillations by supplying an additional feedback stabilizing signal. The PSS modeling approach is shown in Figure 1.

Figure 1. Illustration of PSS lead-lag type
A Novel Modified Black‑Winged Kite Algorithm (MBKA)
In improving this method, we propose a modification of the BKA algorithm. The proposed modification method is to add parameters to monitor the increase in exploration through the number of iterations 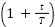 and the average point value of the current solution linked to the
and the average point value of the current solution linked to the 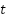 -th iteration
-th iteration 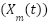 in Eq. (5). So Eq. (5) becomes Eq. (11). By adding dynamic iteration parameters and the influence of the average of group solutions, the algorithm becomes more adaptive and effective in handling complex optimization problems such as PSS tuning. By adding the factor
in Eq. (5). So Eq. (5) becomes Eq. (11). By adding dynamic iteration parameters and the influence of the average of group solutions, the algorithm becomes more adaptive and effective in handling complex optimization problems such as PSS tuning. By adding the factor 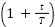 , the algorithm becomes more active in exploring the solution space at the beginning of the iteration, then gradually focuses the search around the best solution. By modifying the way the particle position is updated adaptively based on iterations and probability conditions, the algorithm becomes more intelligent in adjusting the search strategy.
, the algorithm becomes more active in exploring the solution space at the beginning of the iteration, then gradually focuses the search around the best solution. By modifying the way the particle position is updated adaptively based on iterations and probability conditions, the algorithm becomes more intelligent in adjusting the search strategy.
| 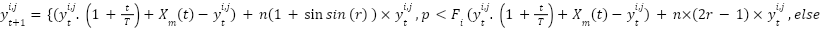
| (11) |
Algorithm : modified Black‑winged kite algorithm (MBKA) |
Input: Population size, Maximum number of iteration, Number of dimension Output: The Best Solution, Objective Function |
1: procedure MBKA 2: Initialize the parameters 3: Set 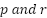 4: Calculate of Fitness value 5: while (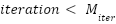 ) ) 6: Assaultive Conduct 7: If (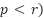 8: 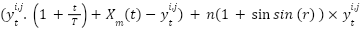 9: else if 10: 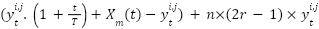 11: End If 12: Migration behavior 13: If (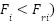 | 14: 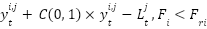 15: else if 16: 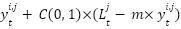 17: End If 18: Select The Best Individual 19: If (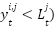 20: 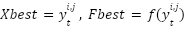 21: else if 22: 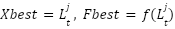 23: End If 24: End While 25: return 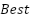 Soluton Soluton 26: End procedure |
RESULTS AND DISCUSSION
Convergence Curve Profile
The MBKA method code is written using the Matlab/Simulink application on a laptop with 8 GB of RAM and an Intel I5-5200 CPU running at 2.19 GHz in 64-bit mode. To determine the ideal power system stabilizer parameters, the PDOMPA is used. Twenty-three benchmark functions were tested in order to assess the PDOMPA's performance. Three categories make up the benchmark function: unimodal (F1-F7), multimodal (F8-F13) and multimodal with fixed dimensions (F14-F23 ). Each of the three groups has distinct qualities. The unimodal function is an excellent candidate for benchmarking algorithm exploitation since it has one global ideal and no local optimality. Because the multi-modal function contains a high number of local optimum points, it is very helpful for evaluating exploration and determining the algorithm's local optima position. The composite function is made up of multi-modal test functions that have been biased, rotated, and shifted. To determine whether MBKA outperforms the competition algorithms statistically, the performance of the two algorithms is compared. The rank of each function can be used to get the mean rank value of any algorithm. Table 1 shows the statistical analysis for each function. A rating is a number that stands for the optimal mean value. The cumulative rank value for each algorithm indicates that MBKA has a value of 1. The average rank value is 1.217391. Table 2 displays a comparison of the ranks of unimodal algorithm functions. MBKA is ranked first in multimodal. A comparison of the multimodal functions used in terms of rankings is shown in Table 3. Table 4 presents a comparison of fixed-multimodal ranks between MBKA and BKA.
Table 1. Comparison of BKA and MBKA
Function | BKA | MBKA | F1 | Best | 8.22E-06 | 5.44E-19 | Mean | 6.68E-02 | 3.72E-14 | Worst | 3.01E+00 | 1.24E-12 | Std | 4.26E-01 | 1.80E-13 | Rank | 2 | 1 | F2 | Best | 1.04E-03 | 2.21E-11 | Mean | 3.64E-02 | 2.92E-08 | Worst | 0.62106 | 1.93E-07 | Std | 0.089576 | 4.56E-08 | Rank | 2 | 1 | F3 | Best | 1.19E-05 | 3.90E-18 | Mean | 2.69E-01 | 1.11E-12 | Worst | 7.44E+00 | 1.67E-11 | Std | 1.18E+00 | 3.01E-12 | Rank | 2 | 1 | F4 | Best | 8.61E-04 | 7.53E-11 | Mean | 2.42E-02 | 9.38E-09 | Worst | 0.246 | 8.56E-08 | Std | 4.26E-02 | 1.55E-08 | Rank | 2 | 1 | F5 | Best | 28.8718 | 2.14E-05 | Mean | 29.4106 | 0.20743 | Worst | 41.2644 | 0.43607 | Std | 1.8 | 0.098827 | Rank | 1 | 1 | F6 | Best | 3.7049 | 2.58E-10 | Mean | 5.6964 | 0.000114 | Worst | 7.7704 | 0.000227 | Std | 0.84945 | 5.63E-05 | Rank | 2 | 1 | F7 | Best | 0.000182 | 1.54E-05 | Mean | 0.007139 | 0.001248 | Worst | 0.033693 | 0.004569 | Std | 0.007384 | 0.001059 | Rank | 2 | 1 | F8 | Best | -7502.6 | -12569.5 | Mean | -5418.66 | -12422 | Worst | -4069.68 | -9576.16 | Std | 815.2733 | 555.0146 | Rank | 1 | 1 | F9 | Best | 1.06E-06 | 0 | Mean | 2.67E+01 | 1.17E-13 | Worst | 1.99E+02 | 5.00E-12 | Std | 6.16E+01 | 7.10E-13 | Rank | 2 | 1 | F10 | Best | 7.16E-04 | 8.88E-16 | Mean | 2.33E-02 | 1.06E-08 | Worst | 0.24525 | 7.69E-08 | Std | 4.30E-02 | 1.59E-08 | Rank | 2 | 1 | F11 | Best | 5.67E-05 | 0 | Mean | 6.19E-02 | 1.13E-14 | Worst | 1.20E+00 | 2.72E-13 | Std | 1.98E-01 | 4.06E-14 | Rank | 2 | 1 |
|
Function | BKA | MBKA | F13 | Best | 1.6456 | 1.50E-09 | Mean | 2.8887 | 8.52E-05 | Worst | 4.0924 | 0.000253 | Std | 0.42646 | 5.39E-05 | Rank | 2 | 1 | F14 | Best | 0.998 | 0.998 | Mean | 1.3742 | 0.998 | Worst | 6.9033 | 0.99804 | Std | 1.0529 | 4.76E-06 | Rank | 2 | 1 | F15 | Best | 0.000308 | 0.000307 | Mean | 0.002924 | 0.000526 | Worst | 0.022553 | 0.002252 | Std | 0.006057 | 0.000411 | Rank | 2 | 1 | F16 | Best | -1.0316 | -1.0316 | Mean | -1.0316 | -1.0316 | Worst | -1.0316 | -1.0314 | Std | 2.17E-07 | 3.13E-05 | Rank | 1 | 2 | F17 | Best | 0.39789 | 0.39789 | Mean | 0.39789 | 0.39801 | Worst | 0.39793 | 0.40282 | Std | 6.30E-06 | 0.000699 | Rank | 1 | 2 | F18 | Best | 3 | 3 | Mean | 3 | 3.0279 | Worst | 0 | 0 | Std | 0 | 0 | Rank | 0 | 0 | F19 | Best | -3.8628 | -3.8628 | Mean | -3.8627 | -3.8613 | Worst | -3.8602 | -3.8447 | Std | 0.000399 | 0.003371 | Rank | 1 | 2 | F20 | Best | -3.3219 | -3.3116 | Mean | -3.221 | -3.139 | Worst | -3.0467 | -2.4649 | Std | 0.082176 | 0.14967 | Rank | 1 | 2 | F21 | Best | -10.1529 | -10.1532 | Mean | -8.7159 | -10.1358 | Worst | -2.612 | -10.0535 | Std | 2.58 | 0.018867 | Rank | 2 | 1 | F22 | Best | -10.4028 | -10.4028 | Mean | -8.3425 | -10.3867 | Worst | -1.8374 | -10.2984 | Std | 2.9803 | 0.021812 | Rank | 2 | 1 | F23 | Best | -10.5364 | -10.5364 | Mean | -8.7322 | -10.5225 | Worst | -2.4215 | -10.4725 | Std | 2.7263 | 0.016128 | Rank | 2 | 1 | Sum Rank | 39 | 28 | Mean Rank | 1.695652 | 1.217391 |
|
Table 2. Rank comparison of unimodal functions between algorithms (F1-F7)
Function | BKA | MBKA |
Sum Rank | 13 | 7 |
Mean Rank | 1.8571429 | 1 |
Total Rank | 2 | 1 |
Table 3. Rank comparison of multimodal functions between algorithms (F8-F13)
Function | BKA | MBKA |
Sum Rank | 11 | 6 |
Mean Rank | 1.8333333 | 1 |
Total Rank | 2 | 1 |
Table 4. Rank comparison of fixed-multimodal functions between algorithms (F14-F23)
Function | BKA | MBKA |
Sum Rank | 15 | 15 |
Mean Rank | 1.5 | 1.5 |
Total Rank | 1 | 1 |
Implementing MBKA for PSS
Additionally, the PSS parameter was tuned in order to measure the performance of the MBKA. To get parameters that meet the ideal output requirements, MBKA is employed. Table 5 shows the parameters of three types of Power System Stabilizer (PSS), namely PSS-Lead Lag, PSS-BKA, and PSS-MBKA. This article uses multiple case studies to assess a single machine system owned by Heffron-Philips. The case study involves varying the system's load by 20%, 50%, and 90%. The integral of time multiplied absolute error (ITAE) is used to optimize the PSS parameter in the first phase. The design problem's objective function is determined to be ITAE. This is demonstrated by equation (12).
Table 5. Parameters of PSS
Methods | 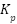
| 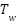
| 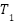
| 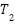
| 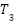
| 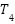
|
PSS-Lead Lag | 0.1123 | 20 | 0.0926 | 0.0926 | 0.0926 | 0.0871 |
PSS-BKA | -100 | 72.68 | 61.4234 | 100 | 5.1783 | 100 |
PSS-MBKA | -100 | 83.4012 | 3.2133 | 100 | -100 | 99.98 |
| 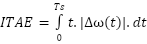
| (12) |
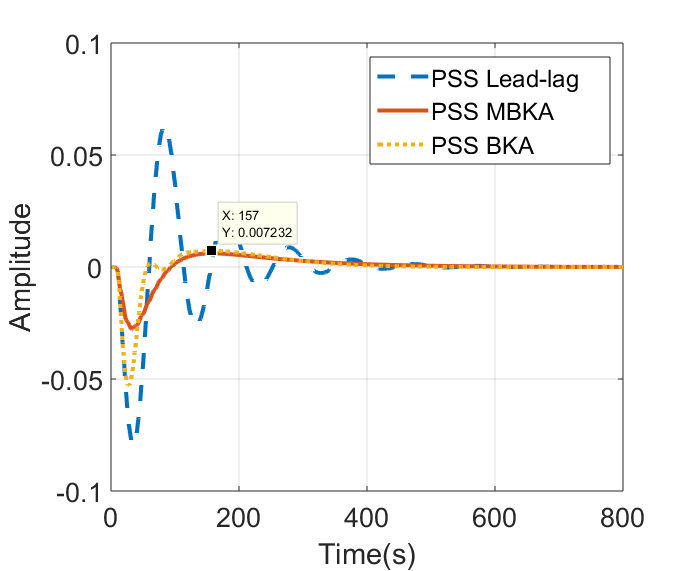
First, the system is subjected to a 20% light load. For every algorithm, a distinct transient response is provided by the system output. See Figure 2(a) for the speed output graph. In Table 6, which illustrates the system response to a 20% load increase disturbance (Case 1), significant performance differences are visible between the three Power System Stabilizer (PSS) methods. The conventional PSS-Lead Lag method shows the weakest performance, with an undershoot of -0.079, an overshoot of 0.062, and the longest settling time of 626 seconds, indicating slow oscillation damping and significant rotor speed fluctuations. Meanwhile, PSS-BKA is able to speed up the stabilization time to 552 seconds and reduce the undershoot to -0.05288, but instead produces a higher overshoot (0.07255), indicating a compromise between response speed and damping smoothness. In contrast, PSS-MBKA provides the best overall performance: it’s undershoot is the smallest (-0.027), its overshoot is almost negligible (0.0061), and its settling time is the shortest (492 seconds). This proves that the modification to the optimization algorithm successfully improves the PSS's ability to dampen rotor speed oscillations quickly and smoothly, making PSS-MBKA the most effective solution for maintaining the dynamic stability of the power system in the face of a 20% load change.
A second case study with a 25% load increase. There is a 50% total load. Figure 2(b) displays the graph from the second case study. In Table 7, which shows the system response to a heavier load disturbance, namely an increase of 50% (Case 2), the performance differences between the three Power System Stabilizer (PSS) methods are even more striking. PSS-Lead Lag, as the conventional method, shows the worst performance with a very large undershoot (-0.1976) and high overshoot (0.1566), as well as a relatively long settling time (602 seconds), indicating that the system experiences strong oscillations and slow recovery due to inadequate damping. On the other hand, PSS-BKA succeeds in significantly reducing the undershoot to -0.137 and suppressing the overshoot to only 0.0182, with a faster settling time (545 seconds), indicating a clear improvement in dynamic stability compared to the conventional method. However, PSS-MBKA provides the best results: the smallest undershoot (-0.0694), an even lower overshoot (0.01526), and the fastest stabilization time (532 seconds). This indicates that PSS-MBKA is not only able to effectively handle large load disturbances, but also provides a smoother and faster response, making it superior in maintaining power system stability even under severe disturbance conditions. In the second case study, the PSS undershoot and overshoot speeds were able to be reduced by 64.88% and 90.25%, respectively, by applying MBKA to the PSS.
In Table 8, which represents the system response to an extreme disturbance in the form of a 90% load increase (Case 3), the performance of the three Power System Stabilizer (PSS) methods again shows significant differences, especially in facing severe stress conditions in the power system. PSS-Lead Lag, as a conventional method, experiences a very large decrease in rotor speed (undershoot), namely -0.3558, accompanied by a high overshoot of 0.2816, as well as the longest settling time (749 seconds), depicting very weak oscillation damping and slow system recovery conditions that could potentially lead to system instability if the disturbance lasts for a long time. In contrast, PSS-BKA shows a significant improvement with a smaller undershoot (-0.2375), a significantly reduced overshoot (0.0323), and a faster settling time (632 seconds), proving the effectiveness of Bat Algorithm-based optimization in improving dynamic response. However, PSS-MBKA once again emerged as the best method: it recorded the lowest undershoot (-0.1271), almost minimal overshoot (0.02744), and the shortest settling time (585 seconds). These results confirm that the modifications to the optimization algorithm in PSS-MBKA are capable of providing much more effective oscillation damping even under extreme load disturbances, making it the most reliable solution for maintaining the dynamic stability of power systems under very challenging operating conditions. Figure 2(c) displays the graph from the second case study. By employing the pump approach, the undershoot and overshoot speed values are 64.28% and 90.26% lower than those obtained with the PSS-Lead Lag method.
Figure 2. Speed in (a) 20% of load (b) 50% of load (c) 90% of load
Table 6. CASE 1: 20 % OF LOAD.
Method
| Speed Response |
Undershoot | Overshoot | Settling Time (s) |
PSS-Lead Lag | -0.079 | 0.062 | 626 |
PSS-BKA | -0.05288 | 0.07255 | 552 |
PSS-MBKA | -0.027 | 0.0061 | 492 |
Table 7. CASE 2: 50 % OF LOAD.
Method
| Speed Response |
Undershoot | Overshoot | Settling Time (s) |
PSS-Lead Lag | -0.1976 | 0.1566 | 602 |
PSS-BKA | -0.137 | 0.0182 | 545 |
PSS-MBKA | -0.0694 | 0.01526 | 532 |
Table 8. CASE 3 : 90 % OF LOAD.
Method
| Speed Response |
Undershoot | Overshoot | Settling Time (s) |
PSS-Lead Lag | -0.3558 | 0.2816 | 749 |
PSS-BKA | -0.2375 | 0.0323 | 632 |
PSS-MBKA | -0.1271 | 0.02744 | 585 |
CONCLUSIONS
The BKA approach has been modified to create MBKA. The meta-heuristic optimization method, Black Kite (BKA) method is inspired by the migration and predatory habits of black kites. To improve the algorithm's capacity for global search and convergence rate, BKA combines Leader and Cauchy mutation strategies. To determine the ideal PSS setting, MBKA is used in this paper. The PSS-Lead Lag approach, the original BKA, and the MBKA method are used to measure and compare the transient response of PSS. Three case studies of load changes are used in the testing. According to the testing results, MBKA applied to PSS can reduce the settlement time, overshoot, and undershoot. The proposed method can reduce the undershoot and overshoot rates by 65% and 90.22% on average compared to the PSS-Lead Lag method, according to the simulation findings using load fluctuations. This research needs to be further developed by incorporating hybrid optimization strategies, particularly by integrating the Lévy Flight algorithm with chaotic methods. The Lévy Flight algorithm is known for its superior exploration capability due to its heavy-tailed step-length distribution, which enables more efficient global search and avoids premature convergence. When combined with chaotic maps, this hybrid approach can significantly balance exploration and exploitation, leading to faster convergence, higher solution accuracy, and greater robustness in complex, high-dimensional search spaces such as those encountered in deep learning hyperparameter optimization or multimodal fusion architectures
ACKNOWLEDGEMENTS
The author would like to express his gratitude for the support provided by Universitas Negeri Surabaya
REFERENCES
- S. Shahzad and E. Jasińska, “Renewable revolution: a review of strategic flexibility in future power systems,” Sustainability, vol. 16, no. 13, p. 5454, 2024, https://doi.org/10.3390/su16135454.
- Y. Zahraoui et al., “AI applications to enhance resilience in power systems and microgrids—A review,” Sustainability, vol. 16, no. 12, p. 4959, 2024, https://doi.org/10.3390/su16124959.
- N. Tatipatri and S. L. Arun, “A comprehensive review on cyber-attacks in power systems: Impact analysis, detection, and cyber security,” IEEE Access, vol. 12, pp. 18147–18167, 2024, https://doi.org/10.1109/ACCESS.2024.3361039.
- A. R. Jordehi, S. A. Mansouri, M. Tostado-Véliz, A. Iqbal, M. Marzband, and F. Jurado, “Industrial energy hubs with electric, thermal and hydrogen demands for resilience enhancement of mobile storage-integrated power systems,” Int. J. Hydrogen Energy, vol. 50, pp. 77–91, 2024, https://doi.org/10.1016/j.ijhydene.2023.07.205.
- B. D. Rosalin, “Energy Monitoring in Wave Power Plant Based on Node-Red and ESP 8266,” Vokasi Unesa Bull. Eng. Technol. Appl. Sci., vol. 1, no. 3, pp. 9–15, 2024, https://doi.org/10.26740/vubeta.v1i3.35456.
- P. Rani, V. Parkash, and N. K. Sharma, “Technological aspects, utilization and impact on power system for distributed generation: A comprehensive survey,” Renew. Sustain. Energy Rev., vol. 192, p. 114257, 2024, https://doi.org/10.1016/j.rser.2023.114257.
- L. Aththanayake, N. Hosseinzadeh, A. Gargoom, and H. H. Alhelou, “Power system reduction techniques for planning and stability studies: A review,” Electr. Power Syst. Res., vol. 227, p. 109917, 2024, https://doi.org/10.1016/j.epsr.2023.109917.
- A. Nawawi, A. Hermawan, and A. Wardani, “Performance of LoRa SX1278 Using Yagi Antenna,” Vokasi Unesa Bull. Eng. Technol. Appl. Sci., pp. 47–58, 2024, https://doi.org/10.26740/vubeta.v1i1.34348.
- M. Amir and K. Singh, “Frequency regulation strategies in renewable energy-dominated power systems: Issues, challenges, innovations, and future trends,” in Advanced Frequency Regulation Strategies in Renewable-Dominated Power Systems, pp. 367–381, 2024, https://doi.org/10.1016/B978-0-323-95054-1.00001-9.
- W. Aribowo, B. Suprianto, and J. Joko, “Improving neural network using a sine tree-seed algorithm for tuning motor DC,” Int. J. Power Electron. Drive Syst., vol. 12, no. 2, p. 1196, 2021, https://doi.org/10.11591/ijpeds.v12.i2.pp1196-1204.
- Y. Li et al., “Artificial intelligence-based methods for renewable power system operation,” Nat. Rev. Electr. Eng., vol. 1, no. 3, pp. 163–179, 2024, https://doi.org/10.1038/s44287-024-00018-9.
- A. Kumar, A. K. Chandel, and S. Tiwari, “Transient Stability Improvement of Multi-Machine System by using STATCOM with Power System Stabilizer,” in 2024 IEEE International Students’ Conference on Electrical, Electronics and Computer Science (SCEECS), pp. 1–5, 2024, https://doi.org/10.1109/SCEECS61402.2024.10482178.
- P. P. Kasaraneni, Y. V. P. Kumar, and R. Kannan, “Data-driven analytics for power system stability assessment,” in Intelligent Data-Driven Modelling and Optimization in Power and Energy Applications, pp. 39–71, 2024, https://doi.org/10.1201/9781003470274.
- M. F. Ma’arif, “Design Lighting System Based on PID Control and Node-RED,” Vokasi Unesa Bull. Eng. Technol. Appl. Sci., vol. 1, no. 3, pp. 1–8, 2024, https://doi.org/10.26740/vubeta.v1i3.35454.
- M. S. Massaoudi, H. Abu-Rub, and A. Ghrayeb, “Navigating the Landscape of Deep Reinforcement Learning for Power System Stability Control: A Review,” IEEE Access, vol. 11, pp. 134298–134317, 2023, https://doi.org/10.1109/ACCESS.2023.3337118.
- M. Khan, W. Wu, and L. Li, “Grid‐forming control for inverter‐based resources in power systems: A review on its operation, system stability, and prospective,” IET Renew. Power Gener., vol. 18, no. 6, pp. 887–907, 2024, https://doi.org/10.1049/rpg2.12991.
- L. Ge et al., “A review of hydrogen generation, storage, and applications in power system,” J. Energy Storage, vol. 75, p. 109307, 2024, https://doi.org/10.1016/j.est.2023.109307.
- A. M. Obais and A. A. Mukheef, “Design of a 120V, 5A SEPIC DC-DC Converter for Unipolar 120V DC Microgrid,” Vokasi Unesa Bull. Eng. Technol. Appl. Sci., vol. 2, no. 3, pp. 655–665, 2025, https://doi.org/10.26740/vubeta.v2i3.44140.
- A. G. Abo-Khalil, “Digital twin real-time hybrid simulation platform for power system stability,” Case Stud. Therm. Eng., vol. 49, p. 103237, 2023, https://doi.org/10.1016/j.csite.2023.103237.
- T. Meridji, G. Joós, and J. Restrepo, “A power system stability assessment framework using machine-learning,” Electr. Power Syst. Res., vol. 216, p. 108981, 2023, https://doi.org/10.1016/j.epsr.2022.108981.
- N. Mira-Gebauer, C. Rahmann, R. Álvarez-Malebrán, and V. Vittal, “Review of wide-area controllers for supporting power system stability,” IEEE Access, vol. 11, pp. 8073–8095, 2023, https://doi.org/10.1109/ACCESS.2023.3237576.
- H. Wang, Z. Xie, Y. Chen, W. Wu, Z. Zhu, and J. Gao, “Stability enhancement control strategy for grid-connected wind power system based on composite feedforward damping,” Int. J. Electr. Power Energy Syst., vol. 158, p. 109908, 2024, https://doi.org/10.1016/j.ijepes.2024.109908.
- D. Butti, S. K. Mangipudi, and S. Rayapudi, “Model order reduction based power system stabilizer design using improved whale optimization algorithm,” IETE J. Res., vol. 69, no. 4, pp. 2144–2163, 2023, https://doi.org/10.1080/03772063.2021.1886875.
- V. Snášel, R. M. Rizk-Allah, D. Izci, and S. Ekinci, “Weighted mean of vectors optimization algorithm and its application in designing the power system stabilizer,” Appl. Soft Comput., vol. 136, p. 110085, 2023, https://doi.org/10.1016/j.asoc.2023.110085.
- W. Aribowo, M. Rohman, F. Baskoro, R. Harimurti, Y. Yamasari, and W. Yustanti, “A Novel Hybrid Prairie Dog Optimization Algorithm-Marine Predator Algorithm for Tuning Parameters Power System Stabilizer,” J. Robot. Control, vol. 4, no. 5, pp. 686–695, 2023, https://doi.org/10.18196/jrc.v4i5.19521.
- W. Aribowo, S. Muslim, Munoto, B. Suprianto, U. T. Kartini, and I. G. P. Asto Buditjahjanto, “Tuning of Power System Stabilizer Using Cascade Forward Backpropagation,” in Proceeding - 2020 3rd International Conference on Vocational Education and Electrical Engineering: Strengthening the framework of Society 5.0 through Innovations in Education, Electrical, Engineering and Informatics Engineering, ICVEE 2020, 2020, https://doi.org/10.1109/ICVEE50212.2020.9243204.
- B. Mushtaq and M. Mufti, “Coordinated operation of fuzzy‐based TCSC and SMES for low‐frequency oscillation damping in interconnected power systems,” Int. J. Circuit Theory Appl., vol. 51, no. 6, pp. 2912–2941, 2023, https://doi.org/10.1002/cta.3543.
- D. U. Sarkar and T. Prakash, "A Recent Review on Approaches to Design Power System Stabilizers: Status, Challenges and Future Scope," in IEEE Access, vol. 11, pp. 34044-34061, 2023, https://doi.org/10.1109/ACCESS.2023.3244687.
- I. I. Addaviqi and A. Prapanca, “Metabharata Game Based on Javanese Wayang Art Using Unity,” Vokasi Unesa Bull. Eng. Technol. Appl. Sci., pp. 38–45, 2024, https://doi.org/10.26740/vubeta.v1i1.34034.
- M. I. Faruqi, “Monitoring of Public Street Lighting Equipment Using Passive Infrared Receiver (PIR) Sensors and Node-red,” Vokasi Unesa Bull. Eng. Technol. Appl. Sci., vol. 1, no. 2, pp. 33–40, 2024, https://doi.org/10.26740/vubeta.v1i2.35411.
- W. J. Ramadhan, A. Amirullah, and A. S. Wardhana, “Telegram Application to Monitor and Control of Automatic Railway Crossing Prototype Using Automatic Transfer Switch,” Vokasi Unesa Bull. Eng. Technol. Appl. Sci., vol. 1, no. 2, pp. 54–63, 2024, https://doi.org/10.26740/vubeta.v1i2.35391.
- W. ARİBOWO, “Comparison Study on Economic Load Dispatch Using Metaheuristic Algorithm,” Gazi Univ. J. Sci., vol. 35, no. 1, p. 1, 2022, https://doi.org/10.35378/gujs.820805.
- Z. Z. A. Thaariq, “Internet of Educational Things (IoET): An Overview,” Vokasi Unesa Bull. Eng. Technol. Appl. Sci., vol. 1, no. 2, pp. 81–92, 2024, https://doi.org/10.26740/vubeta.v1i2.35886.
- M. Hemeida, D. Osheba, S. Alkhalaf, A. Fawzy, M. Ahmed, and M. Roshdy, “Optimized PID controller using Archimedes optimization algorithm for transient stability enhancement,” Ain Shams Eng. J., vol. 14, no. 10, p. 102174, 2023, https://doi.org/10.1016/j.asej.2023.102174.
- M. A. El-Dabah, M. H. Hassan, S. Kamel, M. A. Abido, and H. M. Zawbaa, “Optimal Tuning of Power System Stabilizers for a Multi-Machine Power Systems Using Hybrid Gorilla Troops and Gradient-Based Optimizers,” IEEE Access, vol. 11, pp. 27168–27188, 2023, https://doi.org/10.1109/ACCESS.2023.3250384.
- Y. Wu, S. Fan, P. Liu, J. Sun, T. Lei, and S. Li, “On Optimization of Multi-machine PSS Parameters Tuning Based on SCSO Algorithm,” in 2023 International Conference on Neuromorphic Computing (ICNC), pp. 435–440, 2023, https://doi.org/10.1109/ICNC59488.2023.10462750.
- Z. Sun, Y. Cao, Z. Wen, Y. Song, and Z. Sun, “A Grey Wolf Optimizer algorithm based fuzzy logic power system stabilizer for single machine infinite bus system,” Energy Reports, vol. 9, pp. 847–853, 2023, https://doi.org/10.1016/j.egyr.2023.04.365.
- J. Wang, W. Wang, X. Hu, L. Qiu, and H. Zang, “Black-winged kite algorithm: a nature-inspired meta-heuristic for solving benchmark functions and engineering problems,” Artif. Intell. Rev., vol. 57, no. 4, pp. 1–53, 2024, https://doi.org/10.1007/s10462-024-10723-4.
- D. Chitara, P. K. Singhal, S. L. Surana, G. Sharma, and R. C. Bansal, “Robust multi-machine power system stabilizer design using bio-inspired optimization techniques and their comparison,” Int. J. Electr. Power Energy Syst., vol. 155, p. 109615, 2024, https://doi.org/10.1016/j.ijepes.2023.109615.
- P. Dey et al., “Small signal stability enhancement of large interconnected power system using grasshopper optimization algorithm tuned power system stabilizer,” in Advances in Computers, vol. 135, pp. 99-125, 2024, https://doi.org/10.1016/bs.adcom.2023.11.004.
AUTHOR BIOGRAPHY

| Widi Aribowo     is a lecturer in the Department of Electrical Engineering, Universitas Negeri Surabaya, Indonesia. He is received the BSc from the Sepuluh Nopember Institute of Technology (ITS) in Power Engineering, Surabaya in 2005. He is received the M.Eng from the Sepuluh Nopember Institute of Technology (ITS) in Power Engineering, Surabaya in 2009. He is mainly research in the power system and control. He can be contacted at email: widiaribowo@unesa.ac.id. is a lecturer in the Department of Electrical Engineering, Universitas Negeri Surabaya, Indonesia. He is received the BSc from the Sepuluh Nopember Institute of Technology (ITS) in Power Engineering, Surabaya in 2005. He is received the M.Eng from the Sepuluh Nopember Institute of Technology (ITS) in Power Engineering, Surabaya in 2009. He is mainly research in the power system and control. He can be contacted at email: widiaribowo@unesa.ac.id. |
|
|

| Laith Abualigah     is an Associate Professor at the Department of Computer Science, Al Al-Bayt University, Jordan. He received the Ph.D. degree from the School of Computer Science in Universiti Sains Malaysia (USM), Malaysia in 2018. His main research interests focus on bio-inspired computing, artificial intelligence, metaheuristic modeling, and optimization algorithms, evolutionary computations, information retrieval, feature selection, combinatorial problems, optimization, and NLP. He can be contacted at email: aligah.2020@gmail.com. is an Associate Professor at the Department of Computer Science, Al Al-Bayt University, Jordan. He received the Ph.D. degree from the School of Computer Science in Universiti Sains Malaysia (USM), Malaysia in 2018. His main research interests focus on bio-inspired computing, artificial intelligence, metaheuristic modeling, and optimization algorithms, evolutionary computations, information retrieval, feature selection, combinatorial problems, optimization, and NLP. He can be contacted at email: aligah.2020@gmail.com. |
|
|

| Diego Oliva     is an Associate Professor at the University of Guadalajara in Mexico. He has the distinction of National Researcher Rank 2 by the Mexican Council of Science and Technology. Currently, he is a Senior member of the IEEE. His research interests include evolutionary and swarm algorithms, hybridization of evolutionary and swarm algorithms, computational intelligence, and image processing. He can be contacted at email: diego.oliva@cucei.udg.mx. is an Associate Professor at the University of Guadalajara in Mexico. He has the distinction of National Researcher Rank 2 by the Mexican Council of Science and Technology. Currently, he is a Senior member of the IEEE. His research interests include evolutionary and swarm algorithms, hybridization of evolutionary and swarm algorithms, computational intelligence, and image processing. He can be contacted at email: diego.oliva@cucei.udg.mx. |
|
|

| Nur Vidia Laksmi B     received her B.A.Sc. degree from the Electronic Engineering Polytechnic Institute of Surabaya, Indonesia, in 2015 and her M.Sc. degree form the Department of Electrical Engineering, National Taiwan University of Science and Technology (NTUST), Taiwan, in 2018. Currently, she is a lecturer in the Department of Electrical Engineering, Universitas Negeri Surabaya, Surabaya, Indonesia. Her research interest includes power electronics, motor drives, and the application of control theories. She can be contacted at email: nurvidialaksmi@unesa.ac.id. received her B.A.Sc. degree from the Electronic Engineering Polytechnic Institute of Surabaya, Indonesia, in 2015 and her M.Sc. degree form the Department of Electrical Engineering, National Taiwan University of Science and Technology (NTUST), Taiwan, in 2018. Currently, she is a lecturer in the Department of Electrical Engineering, Universitas Negeri Surabaya, Surabaya, Indonesia. Her research interest includes power electronics, motor drives, and the application of control theories. She can be contacted at email: nurvidialaksmi@unesa.ac.id. |
|
|

| Fithrotul Irda Amaliah     is a lecturer in the Department of Electrical Engineering, Universitas Negeri Surabaya, Indonesia. She is received the S.Tr.T. in Electronics Engineering from the Electronic Engineering Polytechnic Institute of Surabaya (PENS) in 2021. She is received the M.Tr.T. in Electrical Engineering from the Electronic Engineering Polytechnic Institute of Surabaya (PENS) in 2024. She is mainly research in the electronic and sensor. She can be contacted at email: fithrotulamaliah@unesa.ac.id. is a lecturer in the Department of Electrical Engineering, Universitas Negeri Surabaya, Indonesia. She is received the S.Tr.T. in Electronics Engineering from the Electronic Engineering Polytechnic Institute of Surabaya (PENS) in 2021. She is received the M.Tr.T. in Electrical Engineering from the Electronic Engineering Polytechnic Institute of Surabaya (PENS) in 2024. She is mainly research in the electronic and sensor. She can be contacted at email: fithrotulamaliah@unesa.ac.id. |
|
|

| As’ad Shidqy Aziz     is a lecturer in the Department of Electrical Engineering, Universitas Negeri Surabaya, Indonesia. He is received the S.T. from Brawijaya University in Electrical Engineering, Surabaya in 2014. He is received the M.T. from Brawijaya University in Electrical Engineering, Surabaya in 2019. He is mainly research in the Electronics and Sensors. He can be contacted at email: asadaziz@unesa.ac.id. is a lecturer in the Department of Electrical Engineering, Universitas Negeri Surabaya, Indonesia. He is received the S.T. from Brawijaya University in Electrical Engineering, Surabaya in 2014. He is received the M.T. from Brawijaya University in Electrical Engineering, Surabaya in 2019. He is mainly research in the Electronics and Sensors. He can be contacted at email: asadaziz@unesa.ac.id. |
|
|

| Hewa Majeed Zangana is an Assistant Professor at Duhok Polytechnic University (DPU) in Iraq, currently pursuing a PhD in ITM at DPU. He has previously served as an Assistant Professor at Ararat Private Technical Institute and a Lecturer at Amedi Technical Institute and Nawroz University. His administrative roles include Curriculum Division Director at DPU and Acting Dean of the College of Computer and IT at Nawroz University. His research interests cover network systems, information security, and intelligent systems. He has published in peer-reviewed journals such as IEEE and serves on various editorial boards and scientific committees, also published multiple books indexed in Scopus with IGI Global. |
Widi Aribowo (Power System Stabilizer Optimization Based on Modified Black‑Winged Kite Algorithm)