ISSN: 2685-9572 Buletin Ilmiah Sarjana Teknik Elektro
Vol. 7, No. 3, September 2025, pp. 608-624
Metaheuristic-Driven Optimisation of Support Vector Regression Models for Precision Control in Unmanned Aerial Vehicle Systems
Hamzah M. Marhoon 1, Rasha Khalid Omar 2, Hussein Al-Rammahi 3, Sarah O. Al-Tahir 4,
Noorulden Basil 5, Benmessaoud Mohammed Tarik 6, Takele Ferede Agajie 7
1 Department of Automation and Artificial Intelligence Engineering, College of Information Engineering,
Al-Nahrain University, Jadriya, Baghdad, Iraq
2 Ministry of Higher Education and Scientific Research, Scientific Research Commission, Baghdad, Iraq
3 Electrical and Computer Engineering, Altinbas University, Istanbul, Türkiye
4 Department of Power Mechanics Engineering Techniques, Technical College of Engineering, Al-Bayan University, Baghdad, Iraq
5 Department of Electrical Engineering, College of Engineering, Mustansiriyah University, Baghdad, Iraq
6 Electrical and Electronics Engineering Faculty, University of Sciences and Technology of Oran, USTO-MB, BP 1505, EL M'Naouer, Oran, 31000, Algeria
7 Department of Electrical and Computer Engineering, Faculty of Technology, Debre Markos University, PO. BOX 269, Debre Markos, Ethiopia
ARTICLE INFORMATION |
| ABSTRACT |
Article History: Received 13 July 2025 Revised 02 October 2025 Accepted 07 October2025 |
| 
Unmanned Aerial Vehicle (UAV) systems are deployed in dynamic and uncertain environments where many traditional control structures, including Proportional–Integral–Derivative (PID) and Linear Quadratic Regulator (LQR) controllers, are unable to provide stability and adaptation. In order to overcome these shortcomings, this work presents a hybrid Support Vector Regression (SVR) model optimised with the Eagle Strategy-Particle Swarm Optimisation (ES-PSO). The proposed framework is tested with high-fidelity simulated flight data on a quadcopter platform, in which throttle, pitch, roll and yaw are provided as control variables and altitude, velocity and orientation are provided as outputs. The ES-PSO algorithm is an algorithm that optimises the global and local hyperparameters of the SVR and makes it more effective at capturing nonlinear dynamics of the input-output process under both nominal and perturbed flight conditions. To compare with benchmarking, standalone SVR, Neural Networks, Decision Trees, Naive Bayes and K-Nearest Neighbour models were executed using the same simulation parameters with no metaheuristic optimisation, and it was made fair. Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and Mean Percentage Error (MPE) quantitative assessments illustrate that the ES-PSO-SVR model has the lowest error in prediction and the highest tracking accuracy compared to all baseline techniques. These results demonstrate how metaheuristic-based learning systems can be used to drive forward the creation of adaptive and intelligent UAV control systems that can perform effectively in challenging operational conditions. |
Keywords: UAV Control System; Hybrid Machine Learning Support; Adaptive Control; Swarm Intelligence; Flight Dynamics; Parameter Optimisation |
Corresponding Author: Hamzah M. Marhoon, Department of Automation and Artificial Intelligence Engineering, College of Information Engineering, Al-Nahrain University, Jadriya, Baghdad, Iraq. Email: hamzah.marhoon@nahrainuniv.edu.iq |
This work is open access under a Creative Commons Attribution-Share Alike 4.0 
|
Citation Document: H. M. Marhoon, R. K. Omar, H. Al-Rammahi, S. O. Al-Tahir, N. Basil, B. M. Tarik, and T. F. Agajie. “Metaheuristic-Driven Optimisation of Support Vector Regression Models for Precision Control in Unmanned Aerial Vehicle Systems,” Buletin Ilmiah Sarjana Teknik Elektro, vol. 7, no. 3, pp. 608-624, 2025, DOI: 10.12928/biste.v7i3.14251. |
INTRODUCTION
The Unmanned Aerial Vehicles (UAVs), which were initially experimental prototypes, are now regarded as an essential device in numerous industries that are too numerous to mention [1]. Their use has now extended into infrastructure inspection, environmental monitoring, aerial surveillance, and topographic mapping and thus their increasing importance in the civilian and the military realms [2]-[5]. With the increased integration of UAVs in both commercial, defence and scientific activities, it has increased the need to ensure highly advanced, adaptable and highly efficient control systems [6][7]. These systems should have the ability to handle the increasing complexity of the UAV missions, and often these missions take place in unstructured and unpredictable conditions [8][9]. The forces due to wind blows, changes in temperature, loss of GPS signals, among others, represent a significant degree of trouble that requires control solutions that are indeed robust but must also be adaptive to varying flight scenarios [10][11]. In addition to that, UAVs also frequently work in regimes where the aerodynamic behaviour is significantly non-linear, and challenging to describe and, therefore, designing a reliable and robust control strategy becomes even more difficult [12].
Common Proportional-Integral-Derivative (PID) controllers, Linear Quadratic Gaussian (LQR) methods are traditional methods used in the process of control over navigation of UAV [13]-[15]. They are applicable when it is possible to understand the dynamics of the system and when the system is relatively predictable. Nevertheless, the traditional approaches fail frequently in the real application of UAVs, such as autonomy in unstructured cluttered space or missions with randomly appearing disturbances. They have a tendency to give suboptimal performance, particularly in the presence of non-linearities, or undetermined uncertainties, and when there is a need for real-time adaptability [16][17]. These shortcomings imply that the process of parameter tuning is trial and error in the sense that controllers must be tuned several times and resulting in inefficiencies and poor performance in the UAV system. Under such circumstances, it is clear that the conventional control systems will not work in offering the degree of flexibility and accuracy needed in carrying out present-day UAV activities [18][20].
To address these issues, modern trends in the field of machine learning (ML) solutions are of major interest [21], especially those involving supervised learning, which may be implemented in the UAV control mechanisms in terms of improved accuracy and flexibility of the control system [22]. Such complex behaviours of a system can be trained using machine learning models, which can in turn predict the future states of the system using the historical observations [23]. Among these, a technique which is based on the concept of support vector machines (SVM) [24], in other words, the Support Vector Regression (SVR) has done fairly well [25]. SVR was well suited to deal with problems of non-linear regressions, and it may be effectively employed in stipulating the intricacies existing behind UAV dynamics. SVR offers a general technique of modelling non-linear relationships that exist between control inputs and system outputs, even in the face of noise and outliers, since it finds the optimum hyperplane within a high-dimensional feature space [26]. This is the capacity to use less information to make generalisations, which is very appealing in the context of UAV control, where the real-time and accurate measurements of all the states are cumbersome [27].
Nonetheless, despite the promising nature of SVR in the application of UAV control, the effectiveness of such a method is heavily reliant on optimal model hyperparameter tuning, consisting of the type of kernel in the method, the hyperparameter values in the regularisation procedure, and the kernel bandwidth. The values of these hyperparameters have a big implication on the accuracy and generalisation of the SVR model. Owing to over-tuning or under-tuning, the UAV control system may be over-fitted, under-fitted or fail to generalise, all of which may compromise adaptability with varying conditions [28]. Typically, the optimal set of hyperparameters according to a certain problem is sought using a random search or some more traditional method such as the grid search. Although they are easy to implement and apply, they are computationally expensive, as well as that they may not guarantee that the global optimum will be attained, particularly in high-dimensional/non-convex optimisation problems [29].
The recently developed metaheuristic optimisation algorithms present a potent and effective solution to tuning the hyperparameters of machine learning models due to these algorithms being inspired by natural processes and phenomena [30]. Such algorithms include the Genetic Algorithms (GA) [32], Particle Swarm Optimisation (PSO) [31], and Ant Colony Optimisation (ACO) [33], which are intended to search the whole search space and do not need the explicit gradient information to find the global solution [34]. An example, such as in GA, is an imitation of the natural selection in which it iteratively transforms a population of solutions to an optimal one. PSO, which is based on the flocking behaviour of a bird, works by searching for the best solution using a swarm of particles and updating these particle positions on the basis of individual experience and the social memory [35]. Based on the foraging behaviour of the ants, ACO is probabilistic in nature and finds an optimum path through complex environments. These metaheuristic algorithms have been proven to be very effective in solving optimisation problems in various areas, and using them to control the UAV systems is not an exception. Combining metaheuristics and SVR, the process of hyperparameter tuning may be automated so that more accurate models or models are created, and, by extension, more stable and precise UAV control systems may be built [36].
The model in Figure 1 is termed a combination of the PSO with the SVR in terms of adaptation that assumes a systematic framework. The given procedure is initiated by the onset of a training set of information, which is then followed by SVR hyperparameters [37]. Firstly, the recurrence is to be designed at counter 1. The second step is parallel training and prediction of numerous SVR modes, then going through the training and the prediction process. An evaluation is then made in terms of a cost function of these models to determine their performance. The findings are inputted into the search mechanisms of the PSO, which looks into the hyperparameter, space-primarily penalty parameters 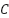 , Epsilon loss parameters (
, Epsilon loss parameters (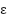 ) and kernel parameters (
) and kernel parameters (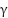 ) in search of superior configurations. Training, evaluation, and hyperparameter optimisation using PSO are used in this loop, which recurs, and there is a counter of recursion in every loop. It stops once a form of restriction position is achieved, which is set beforehand, where the personalised SVR model is completed. Such a recurrence structure will exploit the capabilities of the SVR in strong prediction and PSO in global discovery efficiency and avails coordination to create a high-tuned forecast model [38].
) in search of superior configurations. Training, evaluation, and hyperparameter optimisation using PSO are used in this loop, which recurs, and there is a counter of recursion in every loop. It stops once a form of restriction position is achieved, which is set beforehand, where the personalised SVR model is completed. Such a recurrence structure will exploit the capabilities of the SVR in strong prediction and PSO in global discovery efficiency and avails coordination to create a high-tuned forecast model [38].
This paper constructs and analyses a hybrid control system that combines SVR and Eagle Strategy-Particle Swarm Optimisation to enhance the flexibility and accuracy of UAV flight control. The proposed methodology is initially modelled and simulated in a high-fidelity simulation environment simulating the dynamics of a quadcopter in both nominal and perturbed operating conditions. The paper describes the entire workflow, which consists of data gathering, pre-processing, SVR modelling, and hyperparameter optimisation using Eagle Strategy-Particle Swarm Optimisation (ES-PSO), and performance is evaluated using known error indicators, such as Mean Squared Error (RMSE), Mean Absolute Error (MAE), and Mean Percentage Error (MPE). Comparative testing with standard machine learning models- Neural Networks, Decision trees, Naive Bayes, K-Nearest Neighbours and standalone SVR are done under the same circumstances to provide a fair comparison to test performance. This work will showcase the possibilities of the metaheuristic-based learning models in facilitating robust, adaptable and computationally efficient UAV control systems in dynamic settings by providing access to detailed methodological configurations, empirical findings, and comparisons to existing and popular approaches.
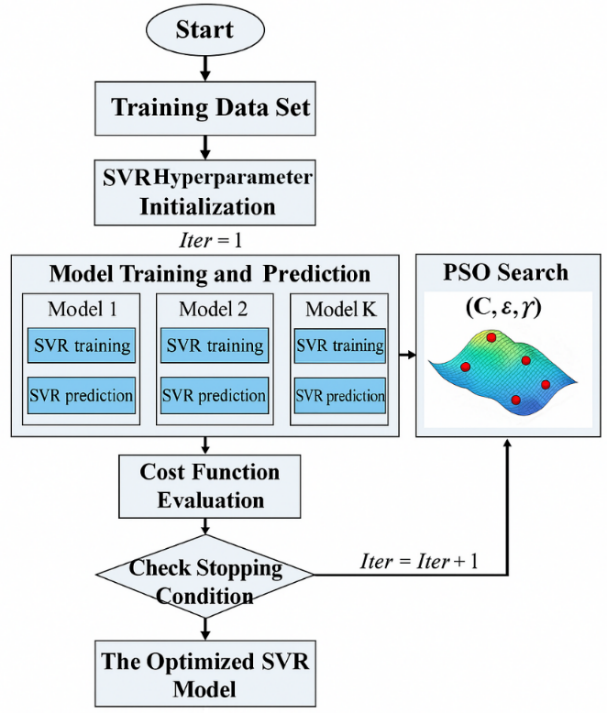
Figure 1. The Hybrid PSO–SVR model structure (redrawn with the copyright of [30])
LITERATURE SURVEY
Over the last few years, research on UAVs has been biased towards hybrid algorithms and particularly SVR and metaheuristic optimisation, specifically PSO, to address the nonlinear nature of aerial systems. This was demonstrated by Su et al. (2024) [39], who reported that PSO-SVR was able to quickly predict the thermal behaviour of spacecraft, with good results regardless of the different test conditions. The study of Huang et al. (2021) [40] in the energy industry demonstrated that PSO-SVR may be used to increase tight-oil recovery prediction accuracy by as much as 85 to more than 96, which highlights the ability to apply it to non-linear physical systems. This synergy has also been adopted with environmental modelling. A hybrid PSO-SVR, named AI-HydSu (Li et al. 2021) [41], was developed to predict dissolved oxygen in aquaculture at a higher convergence and accuracy level. In the meantime, Tian et al. (2024) [42] used Rough Set Theory and PSO-SVR to forecast the emotions of an outdoor micro-space design, which outperformed neural networks and random forests in this regard--a prospect that UAV planners can exploit by considering the aspect of human behaviour regarding surveillance or navigation in urban settings. On the coordination front, Phung and Ha (2020) [43] suggested the Motion-Encoded PSO (MPSO), directly encoding the UAV flight paths within the encryption of the particles in body space, which resulted in a 24% higher detection rate when compared to other approaches and a much-reduced time to search. Shankar et al. (2021) [44] followed a new path with Acceleration-based PSO (APSO), where velocity updates are substituted with acceleration to make it more stable in dynamic and noisy conditions. Hybrid approaches keep on improving: A combination of PSO and Pattern Search by Bao et al. (2013) [45] has been used to fine-tune the SVM parameters, balancing between global and local optimisation. Hoang et al. (2019) [46] investigated angle-encoded PSO on reconfigurable multi-UAV formations, which offers a promising direction in missions that need real-time elasticity and accurate management.
Building on the growing body of work discussed above, research in UAV modelling has steadily shifted from straightforward SVR applications toward more sophisticated PSO–SVR combinations and other metaheuristic-driven solutions. This progression reflects a broader trend: moving beyond static modelling to adaptive, optimisation-oriented frameworks that can cope with the complexity and unpredictability of real flight environments. The works highlighted in Table 1 capture this shift, beginning with early SVR-based modelling and advancing through a range of PSO variants, hybrid architectures, and memetic strategies. Collectively, these contributions have expanded the toolkit for UAV control, improving global search capability, fine-tuning local optimisation, and maintaining robust performance even under challenging operational conditions. What stands out is the versatility of PSO-tuned SVR models, they have been applied successfully to everything from UAV performance forecasting and spacecraft thermal analysis to environmental monitoring and swarm path planning. In each case, the benefits are consistent: faster convergence, stronger generalisation, and greater resilience to uncertainty. Taken together, this evidence forms a compelling rationale for developing the ES–PSO–SVR framework as a next step in intelligent UAV flight control, particularly for demanding tasks like coordinated swarm operations, real-time trajectory planning, and multi-agent navigation in cluttered, dynamic spaces.
Table 1. Summary of key literature on SVR-based UAV control and metaheuristic optimization algorithms.
Authors | Contribution / Focus | Methodology | Findings / Relevance |
Phung & Ha, 2020 | UAV moving target search | Motion-encoded Particle Swarm Optimization (PSO) | Improved search efficiency and accuracy for moving targets in UAV applications. |
Su et al., 2024 | Rapid prediction of spacecraft radiant heat transfer | PSO-SVR hybrid model | High-speed and accurate prediction of heat transfer under vacuum thermal test conditions. |
Huang et al., 2021 | Tight oil recovery prediction | PSO-optimized Support Vector Regression | Demonstrated accurate forecasting of oil recovery rates, improving field decision-making. |
Li et al., 2021 | Dissolved oxygen forecasting in water systems | Hybrid AI model: SVR + PSO | Provided precise predictions of dissolved oxygen levels for environmental monitoring. |
Tian et al., 2024 | Outdoor micro-space design optimization | Rough Set Theory + PSO-SVR | Enabled prolonged human activity by optimizing micro-space layouts, integrating computational intelligence. |
Shankar et al., 2021 | Multi-UAV source-seeking | Acceleration-based PSO | Efficiently guided multiple UAVs to locate sources, showing robustness in multi-agent navigation. |
Bao et al., 2013 | SVM parameter optimization | Memetic Algorithm: PSO + Pattern Search | Improved SVM prediction accuracy by optimizing hyperparameters using hybrid metaheuristics. |
Hoang et al., 2019 | Multi-UAV formation control | Angle-encoded PSO | Achieved flexible and reconfigurable UAV formations, enhancing cooperative UAV missions. |
Predictive Modelling of UAV Systems
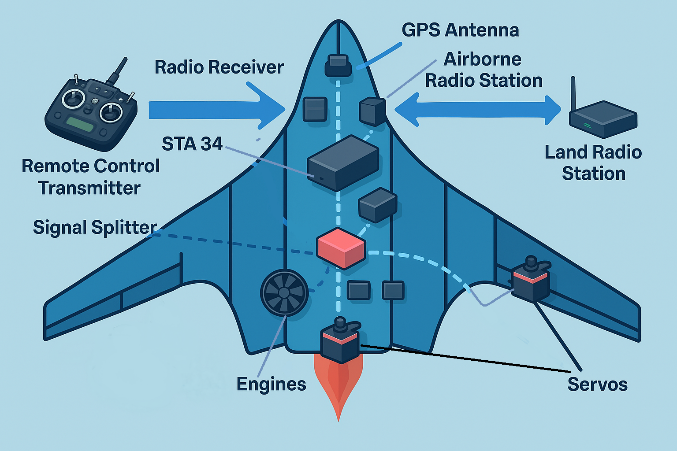
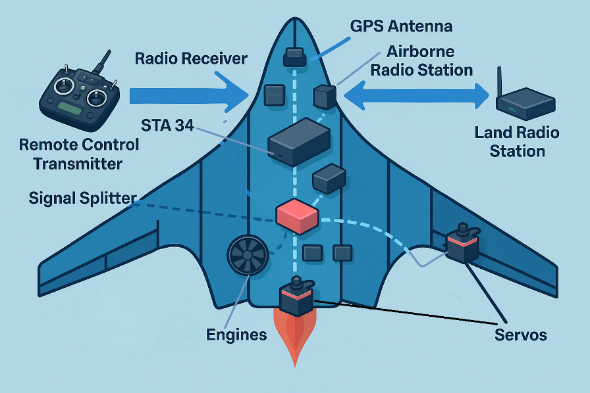
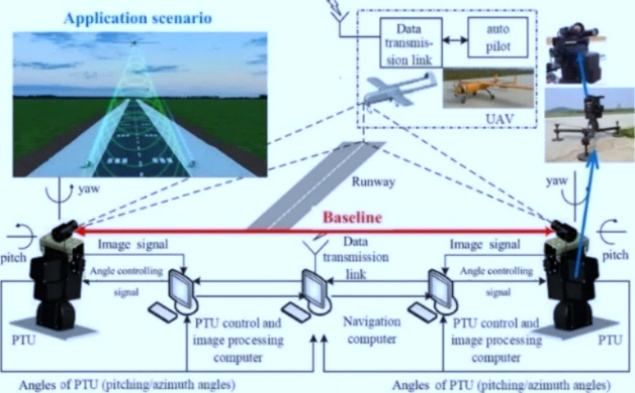
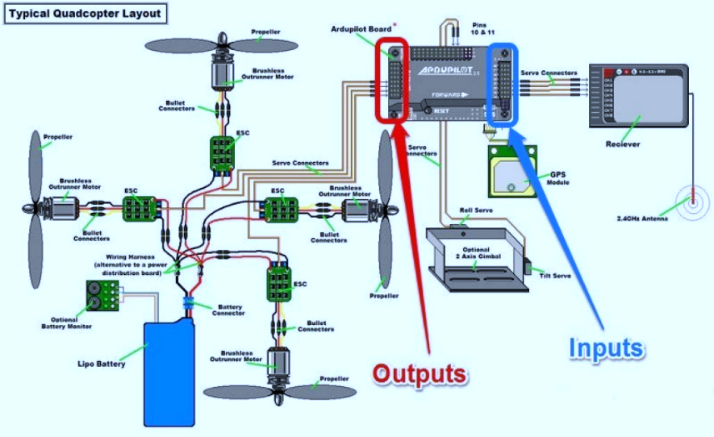
In this section, an advanced model of machine learning-based control, which has the objectives of promoting the adaptability, accuracy, and stability of the UAV systems, is presented. The conventional UAV control systems usually utilise fixed-parameter controllers that could only be tuned manually, and thus the performance of the system may degrade when there is a prevalent and abrupt change in the flight scenario or due to high levels of external disturbances, such as wind gusts, payload influences, sensor noise, etc. These drawbacks impair the immediacy and independence of the UAVs, especially during scenarios in which the mission is crucial, like surveillance, delivery and environmental supervision [47][48]. In order to overcome these constraints, the new framework of control, proposed here, makes use of SVR to develop a model of the highly nonlinear parts of the control input-output relationships (e.g., throttle, pitch, yaw) to control outputs (e.g., position, velocity, orientation). VR can be best applied to this application because it does not require large feature sets to generalise, or a collection of a large number of noisy samples in training, factors that are very common in real flight control onboard systems. Yet, the predictive accuracy of SVRs is very sensitive to the choice of their hyperparameters, such as the regularisation constant (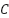 ), parameters of the kernel function, and the epsilon-insensitive loss threshold [49]. Improper settings of such values may result in undesirable performance of the control [50]. To surpass this shortcoming, ES-PSO is used as a worldwide optimisation algorithm for automatic parameter fine-graining. An advantage of the EES-PSO is the possibility to perform the exploratory search characteristic of the Eagle Strategy and to achieve the convergence by fine-tuning the resultant to the PSO. This combination can offer dynamic, adaptive adjustment of the SVR hyperparameters at the real-time level within the controllers and an overall flexible and highly responsive control model that adapts to the given conditions with dynamic flight settings and continuously re-learns its output. To bring practicality to this framework in UAV system design, the whole architecture and flow of communication within a typical UAV control system are depicted in Figure 2. whereas, Figure 2(a) shows the internal connections and signal routing of a quadcopter and the most important components of input and output, with which connection to the flight controller [50]-[58]. While, Figure 2(b) enlarges the illustration to illustrate the communication path between the satellite, ground control, as well as between the UAV and its operators through the transmission and reception of command and telemetry information. Figure 2(c) explains a visual following and guidance case study involving dual Pan-Tilt Unit (PTU) units with image processing that illustrates the need to have accurate control of the angle as part of an autonomous landing or target-tracking on an UAV. Figure 2(d) gives a block diagram of onboard UAV electronics, focusing on the close coupling of sensors, controllers, and actuators in real applications to helical UAVs. All these subfigures will give a complete graphical ground to the application of the ES-PSO-based control model on the application of the ES-PSO-based control model in various UAVs. The hybrid strategy has the advantage of obviating the requirement that the UAV pilot manually tune parameters or utilise preset nominal gains in PID control, and can even be used in the creation of self-optimising UAV platforms that can fly safely and efficiently in unfamiliar, unstructured environments. Such a combination of machine learning and swarm-based optimisation provides a way to create smarter and more autonomous, and robust aerial systems.
), parameters of the kernel function, and the epsilon-insensitive loss threshold [49]. Improper settings of such values may result in undesirable performance of the control [50]. To surpass this shortcoming, ES-PSO is used as a worldwide optimisation algorithm for automatic parameter fine-graining. An advantage of the EES-PSO is the possibility to perform the exploratory search characteristic of the Eagle Strategy and to achieve the convergence by fine-tuning the resultant to the PSO. This combination can offer dynamic, adaptive adjustment of the SVR hyperparameters at the real-time level within the controllers and an overall flexible and highly responsive control model that adapts to the given conditions with dynamic flight settings and continuously re-learns its output. To bring practicality to this framework in UAV system design, the whole architecture and flow of communication within a typical UAV control system are depicted in Figure 2. whereas, Figure 2(a) shows the internal connections and signal routing of a quadcopter and the most important components of input and output, with which connection to the flight controller [50]-[58]. While, Figure 2(b) enlarges the illustration to illustrate the communication path between the satellite, ground control, as well as between the UAV and its operators through the transmission and reception of command and telemetry information. Figure 2(c) explains a visual following and guidance case study involving dual Pan-Tilt Unit (PTU) units with image processing that illustrates the need to have accurate control of the angle as part of an autonomous landing or target-tracking on an UAV. Figure 2(d) gives a block diagram of onboard UAV electronics, focusing on the close coupling of sensors, controllers, and actuators in real applications to helical UAVs. All these subfigures will give a complete graphical ground to the application of the ES-PSO-based control model on the application of the ES-PSO-based control model in various UAVs. The hybrid strategy has the advantage of obviating the requirement that the UAV pilot manually tune parameters or utilise preset nominal gains in PID control, and can even be used in the creation of self-optimising UAV platforms that can fly safely and efficiently in unfamiliar, unstructured environments. Such a combination of machine learning and swarm-based optimisation provides a way to create smarter and more autonomous, and robust aerial systems.
| 
|
- Block Diagram of UAV Communication and Control System Architecture
| - UAV System Architecture with Ground Control Station and Satellite Communication Links
|
| 
|
- UAV-Based Visual Tracking and Navigation System Using Dual PTU Image Processing Units
| - Typical Quadcopter Layout Showing Input and Output Connections with Flight Controller
|
Figure 2. Overall Architecture of UAV Communication, Control, and Propulsion System
SYSTEM SETUP AND DATA ACQUISITION
This section outlines the system context in which the proposed ES-PSO–SVR control model was developed and evaluated. Therefore, due to the complete simulation study, all experimental set-ups, data, and metrics of performance were gathered in the high-fidelity virtual UAV environment. Simulation framework, the process of generating the dataset, and the corresponding preprocessing steps are listed in the following subsections to support the robustness of predictive model training and validation.
UAV Simulation Framework
The control framework was tested using a virtual UAV simulation environment; the model used in the simulation environment mimicked the dynamics of an average UAV platform (quadcopter). The model is developed based on a simulated 6 degrees-of-freedom (6-DoF) multirotor system, as opposed to using hardware available vehicles. As inputs, the control commands provided were throttle, pitch, roll, and yaw, and as the outputs, the flight responses, which were recorded, were position, altitude, velocity, and angular rates. The UAV simulation simulates realistic aerodynamics of the vehicle, actuator behaviour and response delay to represent the physical system characteristics. This configuration gives a secure, reproducible and adaptable environment that can be used to test and verify control strategies, as well as examine system performance across a set of flight conditions. None of the sensors, embedded flight controllers were applied, and all the measurements were produced inside the simulation environment.
Simulation Environment
The modelling and the simulations were performed through MATLAB/Simulink in association with a dynamic flight simulator capable of supporting a realistic quadcopter model. The environment allows fine-tuning of flight parameters in the form of wind disturbances and changes to inertia, sensor noise, etc, which allows tough testing of the control algorithm to be conducted under semi-stochastic conditions. Both the nominal and perturbed flight conditions are simulated as well; therefore, the environment serves to train and benchmark the ES-PSO-SVR model in many different flight behaviours. This method of simulation-driven approaches is repeatable, safe, and scalable, which makes it an excellent choice when developing a control system at an early stage. It should be mentioned that the model was not yet tested on real UAV hardware, but the work will be continued and carried out until the proposed model is implemented in the real world.
Data Acquisition and Structure
The training and evaluation dataset we used is the data record from the simulation during the flight of the UAV under various conditions regarding the UAV control and response. This sample set is composed of about 25,000 time-series elements sampled with a frequency of 100 Hz, and each element of the set relates to a single iteration of a control loop of the UAV. The four control features considered in the input feature matrix (X) are throttle, pitch, yaw and roll. The desired output (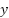 ) contains the UAV response variables, which are the altitude, orientation angle, and velocity. The statistical processing of the data was carried out with the help of Python (pandas’ library). To make it ready to be modelled, all features were normalised using the Min-Max scaling method using the class
) contains the UAV response variables, which are the altitude, orientation angle, and velocity. The statistical processing of the data was carried out with the help of Python (pandas’ library). To make it ready to be modelled, all features were normalised using the Min-Max scaling method using the class 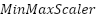 in the package
in the package 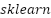 . Preprocessing and the scale of the features became similar. A moving average filter was used to smooth out transient noise and to minimise the effect of outliers. The data was then randomly divided into 70 per cent and 30 per cent, which were to be used in training and testing, respectively. This preprocessed and structured data is used as an empirical source to evaluate the standalone SVR prediction model and its optimised model via the ES-PSO separately, concerning the accuracy of prediction, stability in controlling the model, and generalization abilities.
. Preprocessing and the scale of the features became similar. A moving average filter was used to smooth out transient noise and to minimise the effect of outliers. The data was then randomly divided into 70 per cent and 30 per cent, which were to be used in training and testing, respectively. This preprocessed and structured data is used as an empirical source to evaluate the standalone SVR prediction model and its optimised model via the ES-PSO separately, concerning the accuracy of prediction, stability in controlling the model, and generalization abilities.
PROPOSED METHODOLOGY
The proposed approach presents a two-stage hybrid control system, known as ES-PSO-SVR, to marry the SVR performance of nonlinear regression with the ES-PSO global-local optimisation scheme. The goal of the framework is to make the UAV flight control systems more precise and adaptable to the dynamic environmental and mission-specific conditions of wind disturbance, payload variations, and uncertainty of trajectory. It is a learning model that is founded on data as an alternative to classic PID controllers, as well as manually tuned machine learning models.
SVR-Based Control Modelling
During the initial stage, SVR will be summarised as a supervised machine learning framework to obtain a nonlinear superposition between UAV control commands (e.g., throttle, pitch, roll, and yaw) and their output reactions (e.g., altitude, heading, and velocity) in a non-hypothesised form. By minimizing an 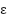 -insensitive loss function, SVR aims to balance model flatness and prediction accuracy. The formulation relies on kernel functions to map the input data into a high-dimensional space, where linear regression is performed. The Radial Basis Function (RBF) kernel is used due to its effectiveness in modeling nonlinear dynamics, and the SVR training process involves optimizing the regularization parameter
-insensitive loss function, SVR aims to balance model flatness and prediction accuracy. The formulation relies on kernel functions to map the input data into a high-dimensional space, where linear regression is performed. The Radial Basis Function (RBF) kernel is used due to its effectiveness in modeling nonlinear dynamics, and the SVR training process involves optimizing the regularization parameter 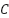 , the epsilon margin
, the epsilon margin 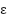 , and the kernel scale
, and the kernel scale 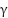 . The full mathematical formulation of SVR is presented in Equations (1) through (4), defining the regression function, kernel transformation, and optimization objective under appropriate constraints. These formulations provide the foundation for precise modelling of UAV dynamics and enable the predictive controller to operate in real time [59][60]. Where, w is the weight vector, x is the input feature vector, b is the bias term,
. The full mathematical formulation of SVR is presented in Equations (1) through (4), defining the regression function, kernel transformation, and optimization objective under appropriate constraints. These formulations provide the foundation for precise modelling of UAV dynamics and enable the predictive controller to operate in real time [59][60]. Where, w is the weight vector, x is the input feature vector, b is the bias term, 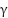 is the kernel width parameter controlling flexibility,
is the kernel width parameter controlling flexibility, 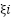 ,
, 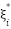 are slack variables,
are slack variables, 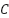 is the regularization constant,
is the regularization constant, 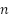 is the number of training samples,
is the number of training samples, 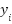 is the true target output, and finally,
is the true target output, and finally, 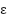 defines the width of the epsilon-insensitive tube.
defines the width of the epsilon-insensitive tube.
Hyperparameter Optimization with ES-PSO
To ensure optimal SVR performance, the second phase of the methodology applies ES-PSO as an automated optimization algorithm. This hybrid approach leverages the global search capability of Eagle Strategy, implemented via Lévy flights, to explore the hyperparameter space broadly, while the local refinement capability of PSO ensures convergence toward high-performing parameter configurations. Each candidate solution in the swarm encodes a triplet 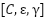 , and model performance is assessed using Root Mean Square Error (RMSE) between predicted and actual UAV responses. Rather than relying on manual or grid-based tuning, ES-PSO adapts the parameter set iteratively based on swarm behaviour and exploratory dynamics. The full optimization configuration, including search ranges, swarm size, inertia weights, and stopping conditions, is provided in Section the following section.
, and model performance is assessed using Root Mean Square Error (RMSE) between predicted and actual UAV responses. Rather than relying on manual or grid-based tuning, ES-PSO adapts the parameter set iteratively based on swarm behaviour and exploratory dynamics. The full optimization configuration, including search ranges, swarm size, inertia weights, and stopping conditions, is provided in Section the following section.
Implementation Workflow
The complete implementation of the ES-PSO–SVR pipeline follows a structured process comprising data import, preprocessing, model initialization, training, optimization, and performance evaluation. Input datasets, consisting of simulated UAV control logs, are pre-processed through normalization and smoothing filters to ensure signal consistency and mitigate noise artifacts. The SVR model is first trained in its baseline form and then re-optimized using the ES-PSO algorithm to enhance control accuracy. Rather than describing each implementation step in isolated figures, the entire computational workflow has been consolidated into Table 2, which outlines each stage of the development pipeline. This tabular representation improves methodological coherence and enhances the transparency and reproducibility of the proposed approach.
Table 2. Workflow summary of the ES-PSO–SVR control system implementation.
Step | Process Stage | Description / Function |
1 | Data Importation | Simulation output data is imported from Excel/CSV files using the Python “ ” library. ” library. |
2 | Feature Selection | Input variables include control commands: throttle, pitch, roll, and yaw. |
3 | Target Definition | Output variables include UAV altitude, velocity, and orientation angle. |
4 | Data Preprocessing | Min-Max normalization and moving average smoothing applied to reduce scale and noise. |
5 | Model Initialization | SVR model is initialized using the scikit-learn SVR class with default parameters. |
6 | Optimization (ES-PSO) | ES-PSO tunes SVR hyperparameters (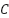 , , 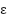 , , 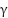 ) based on RMSE using a hybrid global-local search. ) based on RMSE using a hybrid global-local search. |
7 | Training Phase | Optimized SVR is trained on 70% of the data using Python’s 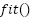 method. method. |
8 | Testing Phase | Model is evaluated on the 30% test set, and performance metrics such as RMSE are computed. |
9 | Comparative Evaluation | Standalone SVR and ES-PSO–SVR results are compared for accuracy and generalization. |
10 | Visualization & Analysis | Results are visualized using matplotlib plots for actual vs predicted outputs. |
PARAMETER SETTINGS AND OPTIMIZATION CONFIGURATION
This section presents the complete configuration settings used for the ES-PSO–SVR control model, including the search ranges for SVR hyperparameters and the internal parameters of the ES-PSO algorithm. Clearly defining these settings is essential for ensuring transparency, reproducibility, and fair benchmarking against baseline models.
SVR Hyperparameter Search Space
The performance of Support Vector Regression is highly sensitive to three key hyperparameters:
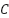 : the regularization parameter that controls the trade-off between model complexity and error tolerance.
: the regularization parameter that controls the trade-off between model complexity and error tolerance.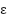 : the epsilon-insensitive loss function margin that defines the error tolerance zone.
: the epsilon-insensitive loss function margin that defines the error tolerance zone.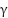 : the kernel coefficient for the Radial Basis Function (RBF) kernel, controlling the influence of single training examples.
: the kernel coefficient for the Radial Basis Function (RBF) kernel, controlling the influence of single training examples.
In order to facilitate the automatic optimisation of the SVR model, the ES-PSO algorithm searches a specific range of values of each hyperparameter, after which the regression modelling is conducted. The latter are the (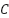 ) for determining the trade-off between model complexity and error tolerance, the epsilon margin (
) for determining the trade-off between model complexity and error tolerance, the epsilon margin (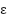 ) determining the width of the non-penalty region of the loss function, and the RBF kernel coefficient (
) determining the width of the non-penalty region of the loss function, and the RBF kernel coefficient (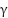 ) affecting the nonlinearity of the RBF kernel. Table 3 presents the exact ranges of values attributed to these hyperparameters. These ranges were chosen using empirical tuning policies and literature suggestions so that those ranges can provide enough diversity to the search space, and can be at least computationally efficient. These values were chosen because of well-established SVR tuning rules and lessons learned in previous experimental investigations, so that there is a reasonable compromise between the model's generalisation power and the control accuracy over different UAV dynamics.
) affecting the nonlinearity of the RBF kernel. Table 3 presents the exact ranges of values attributed to these hyperparameters. These ranges were chosen using empirical tuning policies and literature suggestions so that those ranges can provide enough diversity to the search space, and can be at least computationally efficient. These values were chosen because of well-established SVR tuning rules and lessons learned in previous experimental investigations, so that there is a reasonable compromise between the model's generalisation power and the control accuracy over different UAV dynamics.
Table 3. Search space for SVR hyperparameters used in ES-PSO optimisation
Parameter | Symbol | Search Range | Description |
Regularization | 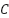
| 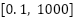
| Controls penalty for model error |
Epsilon | 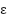
| 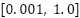
| Margin of error in regression tolerance |
RBF Kernel | 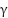
| 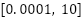
| Controls kernel influence and model flexibility |
ES-PSO Optimisation Parameters
The ES-PSO algorithm consists of the global searching ability of the Eagle Strategy through the use of the Lévy flight mechanism, with local search abilities of the PSO to search and help to tune the hyperparameters of the SVR model in an efficient way. This combination allows searching for general directions at once and approaching quickly and efficiently to find good solutions. The specifications of the ES-PSO algorithm, such as the size of the swarm, inertia weight, learning coefficients and stop conditions have been highlighted in Table 4. The hyperparameters in these settings are set up so that they allow the optimiser to search the hyperparameter search space effectively and with the minimal likelihood of premature convergence. With the addition of Lévy to the Eagle Strategy (ES) component, diversity increases in the population, especially at the early stages of the optimisation process, and helps the algorithm to avoid local minima. However, the PSO mechanism enables the search to have both individual and group experience in refining the candidate solution, resulting in a consistent convergence of the search yielding high-performing SVR settings as opposed to training on average.
Table 4. Configuration parameters of the ES-PSO algorithm for SVR optimization
Parameter | Value | Description |
Population size | 30 | Number of particles (candidate solutions) in the swarm |
Number of generations | 50 | Maximum number of optimization iterations |
Inertia weight | 0.7 | Balances exploration and exploitation in velocity updates |
Cognitive coefficient | 1.5 | Attraction toward particle’s personal best (local knowledge) |
Social coefficient | 1.5 | Attraction toward global best (swarm knowledge) |
Lévy flight step factor | 1.0 | Governs the length of Eagle Strategy exploratory steps |
Stopping criteria | No improvement after 10 iterations OR max generations reached | Terminates if swarm convergence stalls or max iterations are met |
Fitness Evaluation
The quality of every candidate SVR setup is analyzed as the Root Mean Square Error (RMSE) among anticipated and genuine UAV output responses [61], where 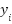 is the actual UAV control output, and
is the actual UAV control output, and 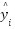 is the SVR-predicted output. This metric was chosen because it directly reflects the accuracy of the control and penalizes large prediction deviations.
is the SVR-predicted output. This metric was chosen because it directly reflects the accuracy of the control and penalizes large prediction deviations.
| 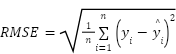
| (5) |
RESULTS AND ANALYSIS
Here we provide the outcomes of performance analysis of the proposed ES-PSO-SVR model and compare the performance of the model with the other machine learning models, including standalone SVR, Decision Tree (DT), Neural Networks, Naïve Bayes and K-nearest neighbours (KNN). We use the important evaluation parameters Measure of Error (ME), Measure of Percentage Error (MPE) and RMSE to evaluate the accuracy of the prediction of the model. The organisation of the discussion is aimed at showing how efficient the ES-PSO-SVR model is in different settings.
Comparative Performance of Models
In Figure 3, the ES-PSO-SVR model is the best performing one as regards ME. This value shows that the ES-PSO-SVR model records the lowest mean error and confirms that the model is the most accurate predictor of any of the conventional machine learning algorithms in place, such as Naive Bayes and KNN, which have substantially higher error rates. Such an outcome demonstrates the effectiveness of employing the ES-PSO algorithm in optimising the hyperparameters of the SVR model to boost its performance in UAV control systems.
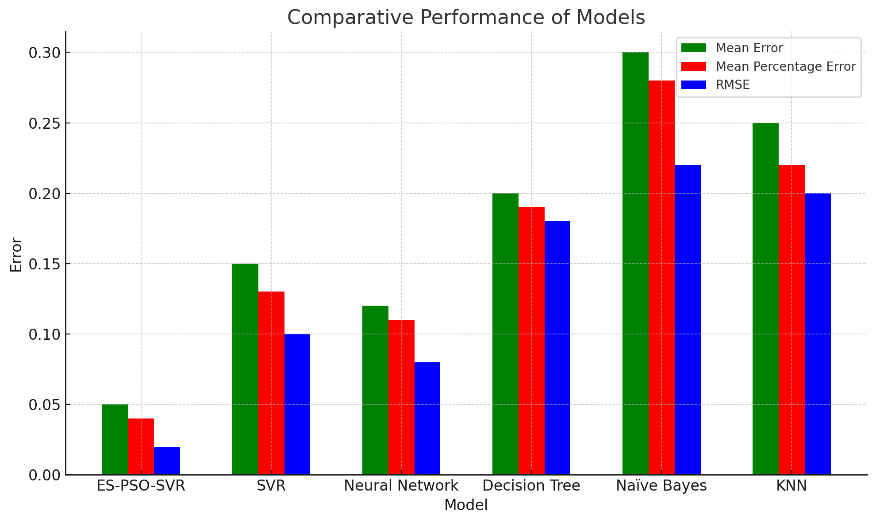
Figure 3. Comparative performance of ES-PSO-SVR and traditional models
Error Comparison Over Time
In order to further assess the soundness and steadiness of the ES-PSO-SVR model, Figure 4 illustrates the error (e.g. RMSE) comparison in time. This plot illustrates that the ES-PSO-SVR scheme shows to have a stable, very low error over different time points, implying that the scheme can be applied to dynamic UAV control systems with ease. Comparatively, such models as Naive Bayes and KNN exhibit greater variation in error over time, which is evidence of less sustained options under varying circumstances. This stability in performance indicates that the fact that ES-PSO-SVR model can be used in real-time applications.
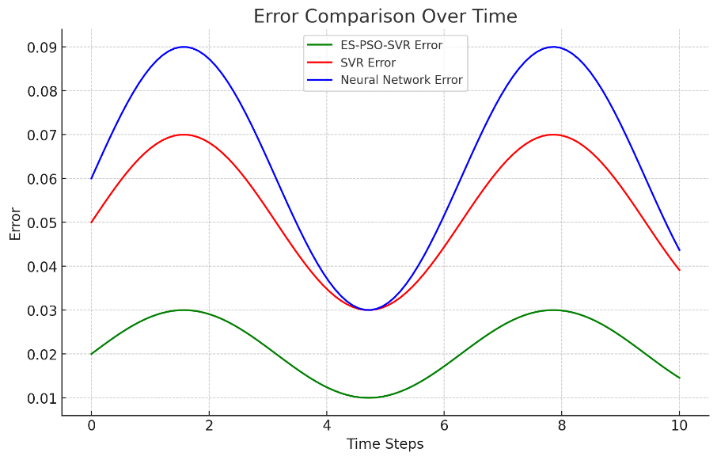
Figure 4. Error comparison over time
Actual vs Predicted Output
Figure 5 contains a plot which compares the actual UAV control outputs with those that are predicted by the ES-PSO-SVR model. The model can be used to closely monitor the actual outputs, indicating how well it can predict the success of UAVs' reaction in real-time. The limited oscillation between the actual and the predicted outputs is additional evidence of the accuracy of the ES-PSO-SVR model, especially in the complex and dynamic flight conditions. The capability of this model to uphold this degree of precision in various scenarios renders this model extremely reliable for autonomous UAV systems.
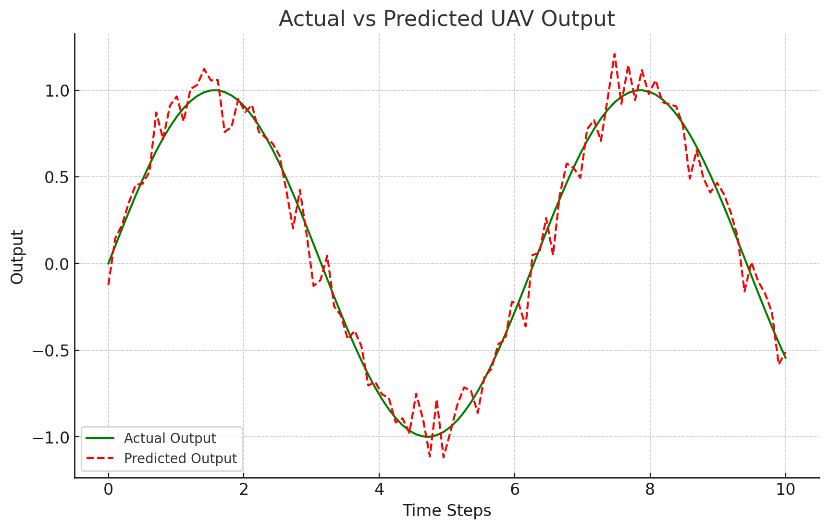
Figure 5. Actual vs. predicted UAV output
Convergence Performance of ES-PSO
The main concern in the optimisation of the ES-PSO-SVR model is the optimisation process. Figure 6 shows the divergence pattern of the ES-PSO algorithm as the generations come and go. As the number of generations grows, the mentioned Figure 6 indicates a consistent decrease in RMSE, indicating that this algorithm is minimising errors with the help of iterative optimisation. This convergence trend indicates the effectiveness of the ES-PSO algorithm in optimising the hyperparameters of the SVR model, which leads to better predictive power.
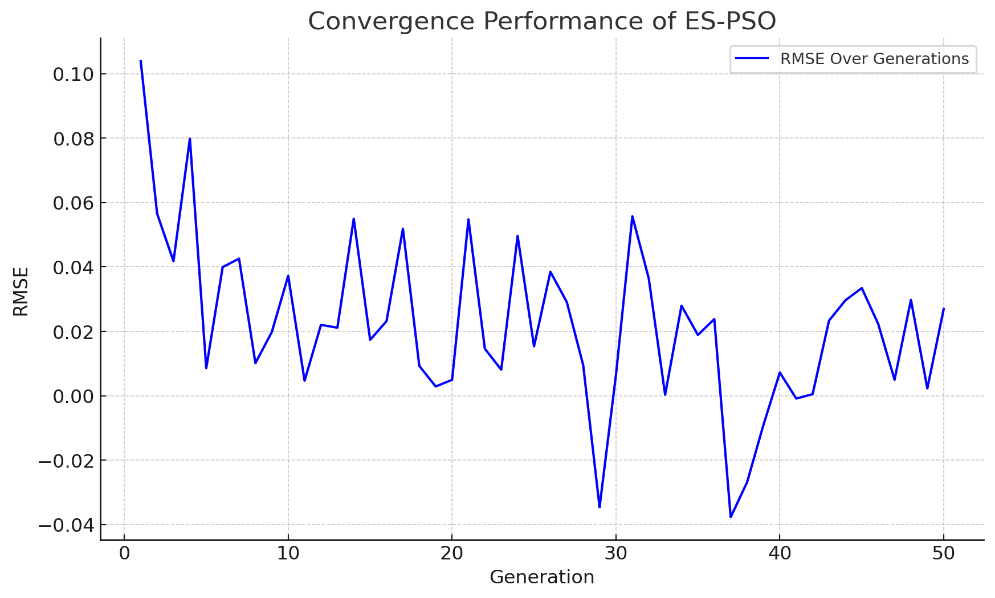
Figure 6. Convergence performance of ES-PSO
Benchmark Function Performance
To answer the question concerning the optimisation capacity of the ES-PSO algorithm, Figures 7 and 8 depict the performance of the given algorithm on generally accepted benchmark functions, such as Sphere, Rastrigin, Rosenbrock and Ackley. Figure 7 illustrates the advantageous performance of the ES-PSO algorithm to converge in good areas on these functions with 3D surface plots. The 3D visualisations indicate that the algorithm is capable of searching high-dimensional solution space, capable of eluding local minima and instead following the global optima. This value highlights the effectiveness of the ES-PSO algorithm in traversing difficult optimisation space, which shows its applicability in tuning hyperparameters of the SVR model. The values of the Sphere benchmark are of particular interest in the current work since it is a commonly studied function when analysing the optimisation research problem and is loosely referred to as a benchmark within the research problem or a reference to evaluate the level of performance of optimisation algorithms. It has a very easy and convex surface with only one global minimum, which enables the optimum algorithm to be run effectively in minimising the objective function. The Sphere functional is used as a threshold in order to determine the basic search and convergence values of the ES-PSO algorithm before any complex functions are tested. It is simple and the landscape of its optimisation is clear; therefore, it is the perfect unit to test the ES-PSO algorithm on its basic efficiency to perform hyperparameter fine-tuning of the SVR model used in UAV control.
Figure 7. Benchmark function performance
Comparing the results, having used the ES-PSO algorithm, 2D plotting was also provided in Figure 8, which shows the results in providing a better performance according to the benchmark functions. Though not a 3D figure, this figure reveals the capability of this algorithm to optimise high-dimensional parameters. The findings of both figures further demonstrate the effectiveness and superiority of the ES-PSO algorithm, which makes it most suited to the optimisation of UAV control systems in which problems of a similar nature in terms of complexity and high dimensionality of parameter space have been previously experienced.
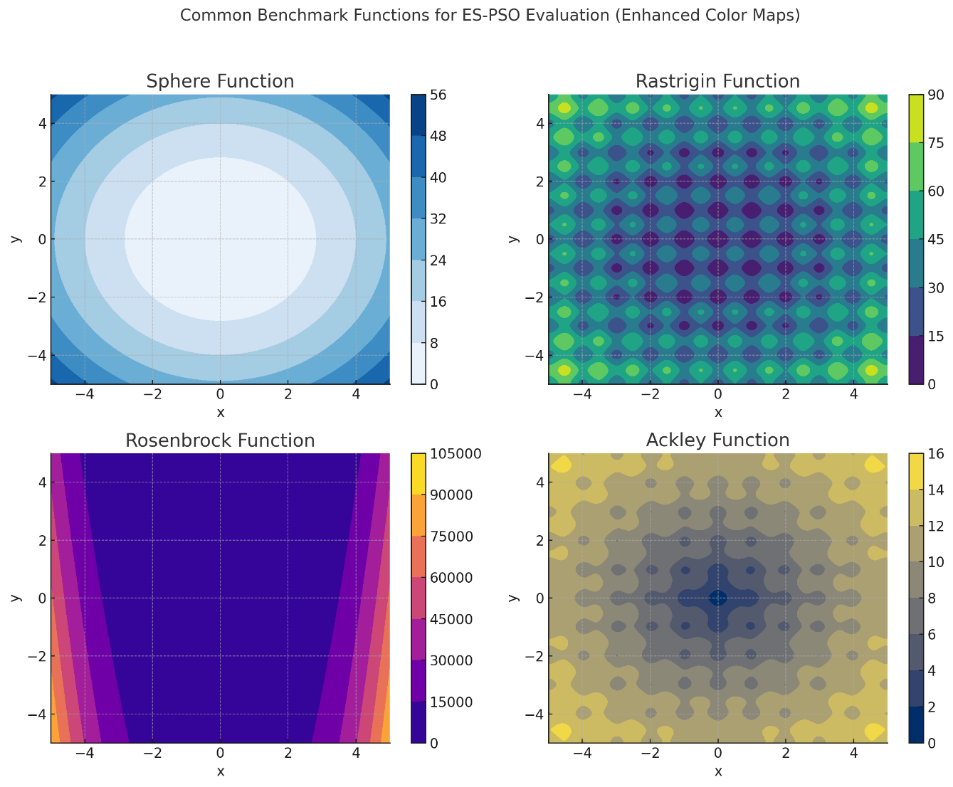
Figure 8. Benchmark functions commonly used for ES-PSO evaluation
Hyperparameter Tuning Visualization
Finally, Figure 9 provides insights into the impact of hyperparameter tuning on the performance of the SVR model. Comparing the results, having used the ES-PSO algorithm, 2D plotting was also provided in Figure 8, which shows the results in providing a better performance according to the benchmark functions. Though not a 3D figure, this figure reveals the capability of this algorithm to optimise high-dimensional parameters. The findings of both figures further demonstrate the effectiveness and superiority of the ES-PSO algorithm, which makes it most suited to the optimisation of UAV control systems in which problems of a similar nature in terms of complexity and high dimensionality of parameter space have been previously experienced. The findings show that the proposed ES-PSO-SVR hybrid algorithm performs better in the modelling of UAV key dynamics, such as the altitude, the pitch, and the velocity. The hybrid method has lower values of error (especially ME, MPE, and RMSE) than baseline methods that include standalone SVR, Decision Trees, Neural Networks, Naive Bayes, and KNN (as shown in Figure 10). But it is important to note that the performance claims are not strongly supported by the comparative analysis, since it is largely done by visual examination and aggregate error values, without testing of confidence limits, multiple-run variance or statistical significance. Moreover, whereas the hybrid model is superior to weaker baselines like Naïve Bayes and KNN, none of these algorithms is considered a state-of-the-art in the time-series control community, and more sophisticated algorithms like LSTMs, Gaussian Processes, or reinforcement learning controllers should be included in future benchmarking to enhance benchmarking rigour. The improvements found can be attributed to the fact that ES-PSO can adaptively adjust the parameters of the regression of the SVR to dynamic UAV behaviour, which can improve predictive accuracy and system resilience. However, the present analysis is simulation-based and is still lacking simulation-based factors relating to real-time implementation, like computational load, inference latency or memory usage, which are key issues of onboard UAV deployment.
Although the results of the proposed ES-PSO-SVR framework are promising, there are a number of limitations that need to be acknowledged. The methodology was only tested in a simulated UAV setting, which, despite its benefits in terms of repeatability and safety, does not allow the recreation of the complexities of the real world, including sensor noise, actuator saturation, communication delays, and unmodeled aerodynamic disturbances. This lack of testing on multiple simulated platforms also limits the testing of robustness with a variety of UAV configurations and operating conditions. Furthermore, although the data preprocessing methods Min-Max scaling and moving average filtering were adopted to normalise and smooth the data set, the effects that those methods had on the retention of the transient dynamics needed for real-time control were not analysed systematically. Concerning optimisation, hyperparameter search spaces of the SVR parameters were not chosen according to empirical practice but according to the formal sensitivity analysis, and the ES-PSO setup was used with fixed parameter values, not investigating their overall impact on the convergence behaviour or computational cost. The lack of an ablation study also does not allow the individual contributions of Eagle Strategy and PSO components to be isolated, and the relative advantage of the hybrid approach has not been proven. Lastly, optimisation was also steered by RMSE alone and no other measures of performance like inference latency, stability margins or computational overhead, which is important in the onboard deployment of UAVs. These constraints demonstrate the necessity of future research incorporating the hardware-in-the-loop testing, expanding the datasets, conducting system-parameter sensitivity analyses, and multi-objective optimisation metrics to identify the generalisability and practical preparedness of the proposed model.
Figure 9. Hyperparameter tuning visualization
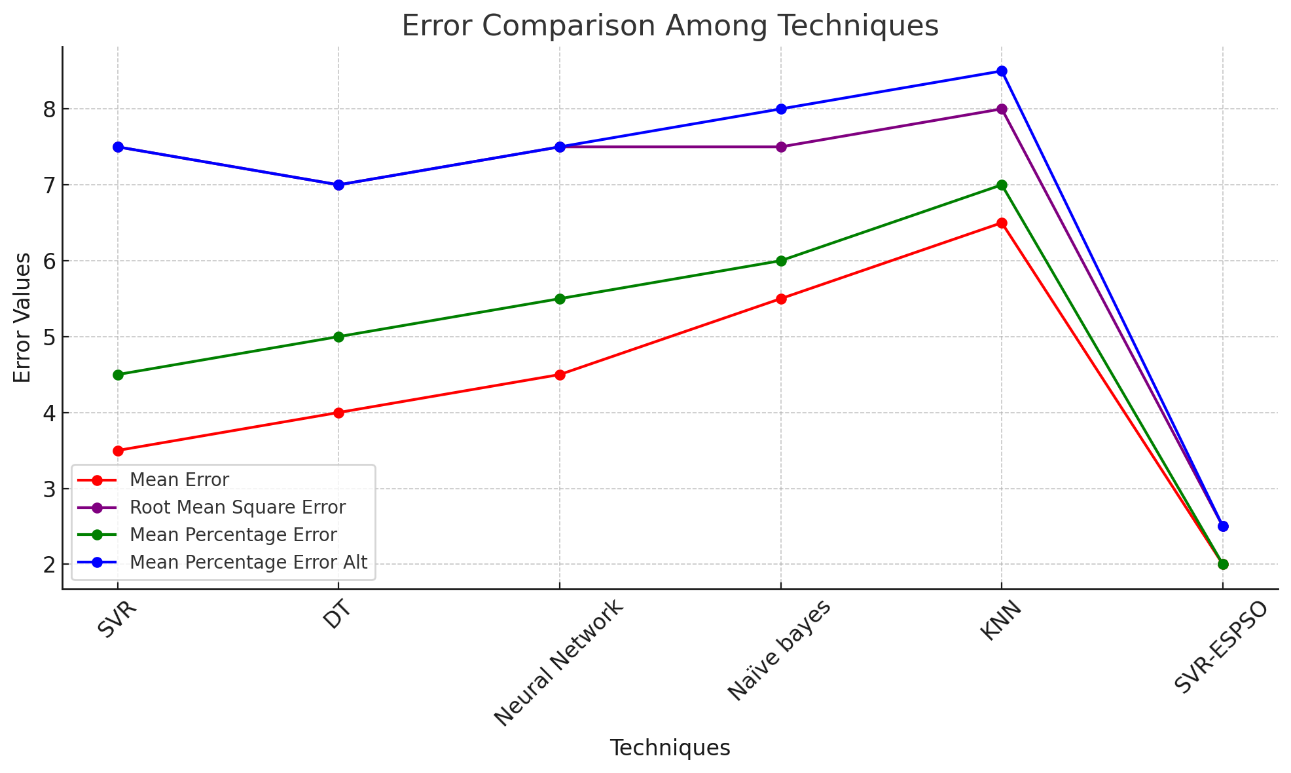
Figure 10. Error metric comparison of ES-PSO–SVR and traditional models
FUTURE INSIGHTS
Based on the existing results, several promising approaches of research can be followed in order to enhance the improvement of both the effectiveness and practical applicability of the SVR-ES-PSO hybrid model in predicting compressive strength of concrete used in civil engineering applications. The reasonable step one can take is to increase the sample size by adding more sizeable and diverse samples based on varied geographical areas and construction conditions. This would enhance the generalisation strength of such a model and reinforce its sturdiness in the presence of various environmental and material situations. Additionally, the advent of advanced deep learning structures, especially Convolutional Neural Networks and Long Short-Term Memory networks, provides an irresistible chance to discover more in-depth non-linear correlations beyond high-dimensional data. The models would supplement the existing method as they can portray more intricate patterns than methods may not take into account. Simultaneously, some feature selection and dimensionality reduction techniques, e.g. Principal Component Analysis (PCA) and Lasso regression, may help reduce the size of the model and identify only the most influential features. This would not only increase computational efficiency but would also increase the interpretability, which is of essence in adoption at the field level.
The other main direction to explore is the use of the SVR-ES-PSO framework with multi-target regression tasks. The model would allow predicting associated properties of concrete, including tensile resistance and durability, all at once, thus helping assess the performance of the construction more comprehensively. Future work can also be done to enable parallel or distributed implementation of the PSO algorithm to support real-time applications. This would lead to enabling converges to be faster and more scalable, especially in large-scale industrial deployments. Lastly, comparative testing against various other metaheuristic optimisers with alternative methods, such as the Modified Particle Swarm Optimisation (M-PSO) and the Ant Lion Optimiser, may provide useful information on the strengths and trade-offs of various optimisation methods to better equip the predictive framework by improving its adaptability and resiliency. Collectively, these lines of research can promote predictive modelling considerably in the field of civil engineering and help construct a more precise, streamlined, and knowledge-curious representation of coming up with concrete strength to meet the technological needs of the modern world.
CONCLUSION
The ES-PSO-SVR hybrid model exhibits encouraging results in the prediction of the dynamic UAV parameters, such as altitude, pitch and velocity, in a simulated setting. Combining Eagle Strategy with PSO to optimise hyperparameters automatically, the framework brings an increase in the predictive accuracy of SVR, and a regular reduction in the values of ME, MPE, and RMSE over the baseline methods that include standalone SVR, Decision Trees, Neural Networks, Naïve Bayes, and KNN. These findings indicate the possibility of enhanced modelling of nonlinear UAV dynamics using metaheuristic-inspired learning techniques. However, the findings are limited in a number of ways to the issue of generalizability and practical applicability. It has only been analysed with synthetic data using one simulation platform, and the model has not been experimented on in real-world UAV deployments where the sensor noise, communication delays, actuator saturation, and unmodeled aerodynamic effects can greatly impair its performance. The comparative evaluation strength is constrained by the dependence on weaker baseline algorithms as well, and further research needs to consider more sophisticated controllers, including LSTMs, Gaussian Processes, or reinforcement learning models. Moreover, although the optimisation process is effective in terms of error minimisation, it also increases the computational cost and convergence is not guaranteed, casting doubt on whether the concept can be practically implemented on board under a real-time performance. Problems like inference latency, memory consumption, chance of overfitting, and insensitivity to hidden disturbances are not considered and must be systematically explored. Considering these reasons, the current research can be considered as a first step towards the implementation of metaheuristic optimisation and regression-based modelling in the area of UAV control.
Author Contribution
All authors contributed equally to the main contributor to this paper. All authors read and approved the final paper.
Conflicts of Interest
The authors declare no conflict of interest.
REFERENCES
- N. Basil et al., "Performance analysis of hybrid optimization approach for UAV path planning control using FOPID-TID controller and HAOAROA algorithm," Sci. Rep., vol. 15, p. 4840, 2025, https://doi.org/10.1038/s41598-025-86803-4.
- A. Mustafa, M. I. Aal-Nouman, and O. A. Awad, "Cloud-based vehicle tracking system," Iraqi J. Inf. Commun. Technol., vol. 2, no. 4, pp. 21–30, 2019, https://doi.org/10.31987/ijict.2.4.81.
- S. A. H. Mohsan, M. A. Khan, F. Noor, I. Ullah, and M. H. Alsharif, "Towards the unmanned aerial vehicles (UAVs): A comprehensive review," Drones, vol. 6, no. 6, p. 147, 2022, https://doi.org/10.3390/drones6060147.
- G. Airlangga, "Advancing UAV path planning system: a software pattern language for dynamic environments," Bul. Ilm. Sarj. Tek. Elektro, vol. 5, no. 4, pp. 475–497, 2023, https://doi.org/10.12928/biste.v5i4.9407.
- G. Airlangga, "Enhancing UAV navigation in dynamic environments: a detailed integration of Fick's law algorithm for optimal pathfinding in complex terrains," Bul. Ilm. Sarj. Tek. Elektro, vol. 5, no. 4, pp. 592–598, 2023, https://doi.org/10.12928/biste.v5i4.9697.
- G. Ariante and G. Del Core, "Unmanned aircraft systems (UASs): Current state, emerging technologies, and future trends," Drones, vol. 9, no. 1, p. 59, 2025, https://doi.org/10.3390/drones9010059.
- Imran and J. Li, "Overview of UAV technology: History and evolution," in UAV Aerodynamics and Crop Interaction, Smart Agriculture, vol. 13. Singapore: Springer, 2025. https://doi.org/10.1007/978-981-96-8402-1_1.
- N. Basil et al., "Multi-criteria decision model for multicircular flight control of unmanned aerial vehicles through a hybrid approach," Sci. Rep., vol. 15, p. 18962, 2025. https://doi.org/10.1038/s41598-025-01508-y.
- Y. Alqudsi and M. Makaraci, "UAV swarms: research, challenges, and future directions," Journal of Engineering and Applied Science, vol. 72, no. 12, 2025, https://doi.org/10.1186/s44147-025-00582-3.
- O. K. Pal et al., "In-depth review of AI-enabled unmanned aerial vehicles: trends, vision, and challenges," Discover Artificial Intelligence, vol. 4, p. 97, 2024, https://doi.org/10.1007/s44163-024-00209-1.
- I. Dagal et al., "Adaptive fuzzy logic control framework for aircraft landing gear automation: optimized design, real-time response, and enhanced safety," International Journal of Aeronautical and Space Sciences, vol. 26, pp. 2135–2163, 2025, https://doi.org/10.1007/s42405-025-00922-w.
- N. Basil, B. M. Sabbar, H. M. Marhoon, A. F. Mohammed, and A. Ma'arif, "Systematic review of unmanned aerial vehicles control: Challenges, solutions, and meta-heuristic optimization," Int. J. Robot. Control Syst., vol. 4, no. 4, 2024, https://doi.org/10.31763/ijrcs.v4i4.1596.
- N. Basil and H. M. Marhoon, "Correction to: selection and evaluation of FOPID criteria for the X-15 adaptive flight control system (AFCS) via Lyapunov candidates: Optimizing trade-offs and critical values using optimization algorithms," e-Prime–Adv. Electr. Eng., Electron. Energy, vol. 8, p. 100589, 2024, https://doi.org/10.1016/j.prime.2024.100589.
- N. Ramadhani, A. Ma'arif, and A. Çakan, "Implementation of PID control for angular position control of Dynamixel servo motor," Control Systems and Optimization Letters, vol. 2, no. 1, pp. 8–14, 2024, https://doi.org/10.59247/csol.v2i1.40.
- Y. Li, R. Lv, and J. Wang, "A control strategy for autonomous approaching and coordinated landing of UAV and USV," Drones, vol. 9, no. 7, p. 480, 2025, https://doi.org/10.3390/drones9070480.
- W. Meng, X. Zhang, L. Zhou, H. Guo, and X. Hu, "Advances in UAV path planning: A comprehensive review of methods, challenges, and future directions," Drones, vol. 9, no. 5, p. 376, 2025, https://doi.org/10.3390/drones9050376.
- R. Roy, M. Islam, N. Sadman, M. A. P. Mahmud, K. D. Gupta, and M. M. Ahsan, "A review on comparative remarks, performance evaluation and improvement strategies of quadrotor controllers," Technologies, vol. 9, no. 2, p. 37, 2021, https://doi.org/10.3390/technologies9020037.
- I. S. Mangkunegara, P. Purwono, A. Ma’arif, N. Basil, H. M. Marhoon, and A. N. Sharkawy, "Transformer models in deep learning: Foundations, advances, challenges and future directions," Bul. Ilm. Sarj. Tek. Elektro, vol. 7, no. 2, pp. 231–241, 2025, https://doi.org/10.12928/biste.v7i2.13053.
- P. Shukla, S. Shukla and A. Kumar Singh, "Trajectory-Prediction Techniques for Unmanned Aerial Vehicles (UAVs): A Comprehensive Survey," in IEEE Communications Surveys & Tutorials, vol. 27, no. 3, pp. 1867-1910, 2025, https://doi.org/10.1109/COMST.2024.3471671.
- L. A. Fagundes-Junior et al., "Machine Learning for Unmanned Aerial Vehicles Navigation: An Overview," SN Computer Science, vol. 5, no. 256, 2024, https://doi.org/10.1007/s42979-023-02592-5.
- Z. Shi, J. Zhang, G. Shi, L. Ji, D. Wang, and Y. Wu, "Design of a UAV Trajectory Prediction System Based on Multi-Flight Modes," Drones, vol. 8, no. 6, p. 255, 2024, https://doi.org/10.3390/drones8060255.
- R. Rajendhiran and A. N, "Hybrid Model for Enhancing Fault Detection System in Nuclear Power Plant using Support Vector Machine and Multivariate State Estimation Techniques," 2025 5th International Conference on Trends in Material Science and Inventive Materials (ICTMIM), pp. 1449-1455, 2025, https://doi.org/10.1109/ICTMIM65579.2025.10988339.
- K. Nazir, Y.-W. Kim, and Y.-C. Byun, "Predictive PID Control for Automated Guided Vehicles Using Genetic Algorithm and Machine Learning," IEEE Access, vol. 13, pp. 66726–66741, 2025, https://doi.org/10.1109/ACCESS.2025.3559072.
- S. Y. Choi and D. Cha, "Unmanned aerial vehicles using machine learning for Autonomous Flight State-of-the-Art," Advanced Robotics, vol. 33, no. 6, pp. 265–277, 2019, https://doi.org/10.1080/01691864.2019.1586760.
- S. MahmoudZadeh, A. Yazdani, Y. Kalantari, B. Ciftler, F. Aidarus, and M. O. Al Kadri, "Holistic Review of UAV-Centric Situational Awareness: Applications, Limitations, and Algorithmic Challenges," Robotics, vol. 13, no. 8, p. 117, 2024, https://doi.org/10.3390/robotics13080117.
- I. Anam, N. Arafat, M. S. Hafiz, J. R. Jim, M. M. Kabir, and M. F. Mridha, "A systematic review of UAV and AI integration for targeted disease detection, weed management, and pest control in precision agriculture," Smart Agricultural Technology, vol. 9, p. 100647, 2024, https://doi.org/10.1016/j.atech.2024.100647.
- N. B. Mohamadwasel and S. Kurnaz, “Implementation of the parallel robot using FOPID with fuzzy type-2 in use social spider optimization algorithm,” Appl. Nanosci., vol. 13, no. 2, pp. 1389–1399, 2023, https://doi.org/10.1007/s13204-021-02034-9.
- S. Shobeiri, "Enhancing transparency in healthcare machine learning models using Shap and Deeplift: A methodological approach," Iraqi J. Inf. Commun. Technol., vol. 7, no. 2, pp. 56–72, 2024, https://doi.org/10.31987/ijict.7.2.285.
- Z. Z. Edie, "Malware detection system based on deep learning technique," Iraqi J. Inf. Commun. Technol., vol. 1, no. 1, pp. 33–44, 2021, https://doi.org/10.31987/ijict.1.1.177.
- N. B. Mohamadwasel and A. Ma’arif, “NB Theory with Bargaining Problem: A New Theory,” Int. J. Robot. Control Syst., vol. 2, no. 3, pp. 606–609, Sep. 2022, https://doi.org/10.31763/ijrcs.v2i3.798.
- N. Abbas et al., "Survey of advanced nonlinear control strategies for UAVs: Integration of sensors and hybrid techniques," Sensors, vol. 24, no. 11, p. 3286, 2024, https://doi.org/10.3390/s24113286.
- G. Airlangga, O. I. A. Nugroho, and L. F. Sugianto, "Comparative evaluation of machine learning models for UAV network performance identification in dynamic environments," Bul. Ilm. Sarj. Tek. Elektro, vol. 6, no. 4, pp. 357–365, 2024, https://doi.org/10.12928/biste.v6i4.12409.
- S. Zhang, H. Yu, B. Tian, X. Wang, W. Cui, L. Yang, J. Li, H. Gong, J. Zhao, L. Lu, J. Zhao, and Y. Lan, "Combining UAV multi-source remote sensing data with CPO-SVR to estimate seedling emergence in breeding sunflowers," Agronomy, vol. 14, no. 10, p. 2205, 2024. https://doi.org/10.3390/agronomy14102205.
- N. Basil et al., "Accelerated black hole optimization algorithm with enhanced FOPID controller for omni-wheel drive mobile robot system," Neural Comput. Appl., vol. 37, pp. 16983–17014, 2025, https://doi.org/10.1007/s00521-025-11310-6.
- S. Selvarajan, "A comprehensive study on modern optimization techniques for engineering applications," Artif. Intell. Rev., vol. 57, p. 194, 2024, https://doi.org/10.1007/s10462-024-10829-9.
- A. O. Alaa, "The optimum design of interval type-2 fuzzy controller for 5 DOF robotic manipulator," Iraqi J. Inf. Commun. Technol., vol. 1, no. 1, pp. 36–51, 2018, https://doi.org/10.31987/ijict.1.1.10.
- Z. S. Bakr, R. F. Hassan, S. O. Al-Tahir, N. Basil, A. Ma’arif, and H. M. Marhoon, "A comparative study of fuzzy logic controller, ANFIS, and HHOPSO algorithms in the LEACH protocol for optimising energy efficiency and network longevity in wireless sensor networks," Int. J. Robot. Control Syst., vol. 5, no. 3, pp. 1678–1700, 2025, https://doi.org/10.31763/ijrcs.v5i3.1918.
- V. H. Nhu et al., "A hybrid computational intelligence approach for predicting soil shear strength for urban housing construction: A case study at Vinhomes Imperia project, Hai Phong city (Vietnam)," Eng. Comput., vol. 36, pp. 603–616, 2020, https://doi.org/10.1007/s00366-019-00718-z.
- M. D. Phung and Q. P. Ha, "Motion-encoded particle swarm optimization for moving target search using UAVs," Appl. Soft Comput., vol. 97, p. 106705, 2020, https://doi.org/10.1016/j.asoc.2020.106705.
- X. Su, H. Jiang, T. Qin, and G. Lin, "Particle Swarm Optimization–Support Vector Regression (PSO-SVR)-Based Rapid Prediction Method for Radiant Heat Transfer for a Spacecraft Vacuum Thermal Test," Appl. Sci., vol. 14, no. 20, p. 9407, 2024, https://doi.org/10.3390/app14209407.
- S. Huang, L. Tian, J. Zhang, X. Chai, H. Wang, and H. Zhang, "Support Vector Regression Based on the Particle Swarm Optimization Algorithm for Tight Oil Recovery Prediction," ACS Omega, vol. 6, no. 47, pp. 32142–32150, 2021, https://doi.org/10.1021/acsomega.1c04923.
- D. Li, X. Wang, J. Sun, and H. Yang, "AI-HydSu: An advanced hybrid approach using support vector regression and particle swarm optimization for dissolved oxygen forecasting," Math. Biosci. Eng., vol. 18, no. 4, pp. 3646–3666, 2021, https://doi.org/10.3934/mbe.2021182.
- J. Tian, Z. Chen, L. Yuan, and H. Zhou, "Optimizing Outdoor Micro-Space Design for Prolonged Activity Duration: A Study Integrating Rough Set Theory and the PSO-SVR Algorithm," Buildings, vol. 14, no. 12, p. 3950, 2024, https://doi.org/10.3390/buildings14123950.
- A. Shankar, H. Kandath, and J. Senthilnath, "Acceleration-based PSO for Multi-UAV Source-Seeking," arXiv preprint arXiv:2109.11462, 2021, https://doi.org/10.48550/arXiv.2109.11462.
- Y. Bao, Z. Hu, and T. Xiong, "A PSO and Pattern Search based Memetic Algorithm for SVMs Parameters Optimization," Neurocomputing, vol. 117, pp. 98–106, 2013, https://doi.org/10.1016/j.neucom.2013.01.027.
- V. T. Hoang, M. D. Phung, T. H. Dinh, Q. Zhu, and Q. P. Ha, "Reconfigurable Multi-UAV Formation Using Angle-Encoded PSO," in Proc. IEEE Int. Conf. Autom. Sci. Eng. (CASE), pp. 1670–1675, 2019, https://doi.org/10.48550/arXiv.1909.03352.
- H. M. Marhoon, A. R. Ibrahim, and N. Basil, "Enhancement of electro hydraulic position servo control system utilising ant lion optimiser," Int. J. Nonlinear Anal. Appl., vol. 12, no. 2, pp. 2453–2461, 2021, https://doi.org/10.22075/ijnaa.2021.5387.
- N. Basil, H. M. Marhoon, and A. F. Mohammed, "Evaluation of a 3-DOF helicopter dynamic control model using FOPID controller-based three optimization algorithms," Int. J. Inf. Technol., pp. 1-10, 2024, https://doi.org/10.1007/s41870-024-02373-0.
- I. A. Hasan and O. A. Awad, "An optimized fuzzy logic controller for wireless network control system using PSO," Iraqi J. Inf. Commun. Technol., vol. 5, no. 1, pp. 1–15, 2022, https://doi.org/10.31987/ijict.5.1.180.
- H. M. Marhoon, N. Basil, and A. Ma’arif, “Exploring Blockchain Data Analysis and Its Communications Architecture: Achievements, Challenges, and Future Directions: A Review Article.,” Int. J. Robot. Control Syst., vol. 3, no. 3, pp. 609–626, 2023, https://doi.org/10.31763/ijrcs.v3i3.1100.
- G. Airlangga, "Optimizing UAV navigation: A particle swarm optimization approach for path planning in 3D environments," Bul. Ilm. Sarj. Tek. Elektro, vol. 5, no. 4, pp. 606–613, 2023, https://doi.org/10.12928/biste.v5i4.9696.
- A. R. Ibrahim, N. Basil, and M. I. Mahdi, “Implementation enhancement of AVR control system within optimization techniques,” Int. J. Nonlinear Anal. Appl., vol. 12, no. 2, pp. 2021–2027, 2021, https://doi.org/10.22075/ijnaa.2021.5339.
- X. Su, H. Jiang, T. Qin, and G. Lin, "Particle Swarm Optimization–Support Vector Regression (PSO-SVR)-Based Rapid Prediction Method for Radiant Heat Transfer for a Spacecraft Vacuum Thermal Test," Appl. Sci., vol. 14, no. 20, p. 9407, 2024, https://doi.org/10.3390/app14209407.
- H. M. Marhoon, N. Basil, and A. F. Mohammed, "Medical Defense Nanorobots (MDNRs): a new evaluation and selection of controller criteria for improved disease diagnosis and patient safety using NARMA(L2)-FOP + D(ANFIS)µ–Iλ-based Archimedes Optimization Algorithm," International Journal of Information Technology, vol. 17, pp. 3935–3945, 2025, https://doi.org/10.1007/s41870-023-01724-7.
- D. Li, "AI-HydSu: An advanced hybrid approach using support vector regression and particle swarm optimization for dissolved oxygen forecasting," Math. Biosci. Eng., vol. 18, no. 4, pp. 3646–3666, 2021, https://doi.org/10.3934/mbe.2021182.
- M. A. Sadi, A. Jamali, and A. M. N. Abang Kamaruddin, "Optimizing UAV performance in turbulent environments using cascaded model predictive control algorithm and Pixhawk hardware," J. Braz. Soc. Mech. Sci. Eng., vol. 47, p. 396, 2025, https://doi.org/10.1007/s40430-025-05693-9.
- A. F. Mohammed, H. M. Marhoon, N. Basil, and A. Ma’arif, "A new hybrid intelligent fractional order proportional double derivative+ integral (FOPDD+I) controller with ANFIS simulated on automatic voltage regulator system," Int. J. Robot. Control Syst., vol. 4, no. 2, 2024, https://doi.org/10.31763/ijrcs.v4i2.1336.
- H. S. Abdulkareem and O. A. Awad, "Fuzzy set-point weight for PID controller based on antlion optimizer to congestion avoidance in TCP/AQM routers," Iraqi J. Inf. Commun. Technol., vol. 2, no. 4, pp. 1–10, 2019, https://doi.org/10.31987/ijict.2.4.73.
- Z. Ma, T. Hu, and L. Shen, "Stereo vision guiding for the autonomous landing of fixed-wing UAVs: A saliency-inspired approach," Int. J. Adv. Robot. Syst., vol. 13, no. 2, p. 43, 2016, https://doi.org/10.5772/62257.
- M. Z. Al-Faiz and A. A. Al-Hamadani, "Analysis and implementation of brain waves feature extraction and classification to control robotic hand," Iraqi J. Inf. Commun. Technol., vol. 1, no. 3, pp. 31–41, 2018, https://doi.org/10.31987/ijict.1.3.35.
- A. Jalili et al., "Performance of various kernel functions for mass prediction with support vector machine," Eur. Phys. J. A, vol. 61, p. 143, 2025, https://doi.org/10.1140/epja/s10050-025-01610-9.
Hamzah M. Marhoon (Metaheuristic-Driven Optimisation of Support Vector Regression Models for Precision Control in Unmanned Aerial Vehicle Systems)