Buletin Ilmiah Sarjana Teknik Elektro ISSN: 2685-9572
Comparative Analysis of PID Tuning Methods for Speed Control in Mecanum-Wheel Electric Wheelchairs
Nuntachai Thongpance 1, Phichitphon Chitikunnan 2, Anantasak Wongkumheang 3,
Rawiphon Chotikunnan 4, Pariwat Imura 5, Wanida Khotakham 6,
Anuchit Nirapai 7, Kittipan Roongprasert 8
1,2,3,4,5,6,7,8 College of Biomedical Engineering, Rangsit University, Pathum Thani, Thailand
ARTICLE INFORMATION |
| ABSTRACT |
Article History: Received 17 March 2025 Revised 24 April 2025 Accepted 28 April 2025 |
| 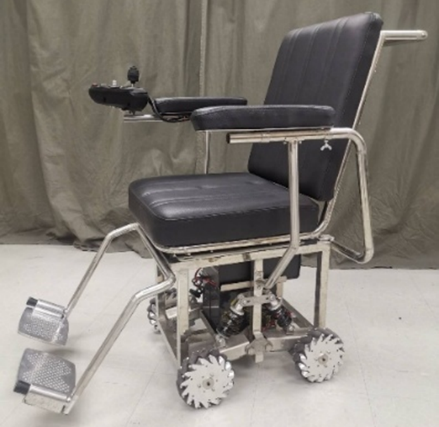
This study compares two PID controller tuning methods, particle swarm optimization (PSO) and Cohen-Coon, employed for speed control of an omnidirectional Mecanum-wheel electric wheelchair. Mecanum wheels improve maneuverability on powered mobility platforms; yet, controlling these systems is difficult due to nonlinearities and directional coupling effects. This work investigates the effectiveness of PSO as a sophisticated alternative to traditional PID tuning methods, effectively tackling this issue. This study evaluates P, PI, PD, and PID controllers tuned by both Cohen-Coon and PSO methods, applied to a DC motor system simulating real-world wheelchair actuation. Step response-based system identification models the motor using MATLAB/Simulink. Simulations of a 12V DC motor are examined using controlled-step time-domain inputs. Every controller configuration is subjected to evaluation for overshoot, root mean square error (RMSE), rise time, and settling time. The PSO-tuned PID controller exhibited enhanced performance, characterized by a rise time of 2.06 s, a settling time of 2.37 s, an overshoot of 0.78%, and an RMSE of 4.59, far surpassing the Cohen-Coon variant, which had a settling time of 6.12 s and an overshoot of 20.14%. The results indicate that PSO enhances both transient and steady-state performance in intricate and disturbance-sensitive systems, including Mecanum wheelchairs. Despite PSO's increased computing complexity during offline tuning and the necessity for meticulous parameter selection, its advantages can be precomputed and effectively utilized in real-time embedded systems. This study highlights the importance of safety, dependability, and responsiveness, illustrating that PSO is a scalable and efficient method for improving assistive robotic systems. |
Keywords: PID Tuning; Cohen-Coon Method; Particle Swarm Optimization (PSO); Assistive Robotics; Embedded Control Systems |
Corresponding Author: Phichitphon Chitikunnan, College of Biomedical Engineering, Rangsit University, Pathum Thani, Thailand. Email: phichitphon.c@rsu.ac.th |
This work is licensed under a Creative Commons Attribution-Share Alike 4.0 
|
Document Citation: N. Thongpance, P. Chitikunnan, A. Wongkumheang, R. Chotikunnan, P. Imura, W. Khotakham, A. Nirapai, and K. Roongprasert, “Comparative Analysis of PID Tuning Methods for Speed Control in Mecanum-Wheel Electric Wheelchairs,” Buletin Ilmiah Sarjana Teknik Elektro, vol. 7, no. 2, pp. 95-110, 2025, DOI: 10.12928/biste.v7i2.13046. |
- INTRODUCTION
The growing global demographic of older citizens and those with mobility problems has resulted in heightened interest in assistive technologies, particularly powered wheelchairs. Although conventional electric wheelchairs provide autonomy, they frequently encounter difficulties maneuvering in restricted inside spaces due to their limited mobility. Mecanum wheels, facilitating omnidirectional movement via angled rollers, have arisen as a solution to this challenge, improving maneuverability in clinical, residential, and hospital environments [1]–[3]. The intricate kinematics and interrelated dynamics of Mecanum-wheel systems present considerable control issues that require sophisticated and adaptive control solutions [4][5].
The proportional-integral-derivative (PID) controller is fundamental in control engineering because of its simplicity and proven efficacy in regulating linear systems [6]–[8]. Traditional PID tuning techniques, like Ziegler-Nichols and Cohen-Coon, remain extensively utilized. The Cohen-Coon technique is particularly preferred for first-order systems with time delays, offering analytical gain settings [9][10]. However, these methodologies demonstrate constraints in intricate, nonlinear systems, such as those utilizing Mecanum wheels, where the presumption of decoupled and linear dynamics fails to hold [11]–[13]. However, limited studies have compared PSO with Cohen–Coon in Mecanum-based wheelchair systems.
Researchers have explored intelligent optimization methods including PSO (Particle Swarm Optimization), Genetic Algorithms (GA), and Differential Evolution (DE) to overcome these limitations. These methodologies are highly effective at solution space exploration and improving performance metrics such as the Integral of Absolute Error (IAE), Integral of Time-weighted Absolute Error (ITAE), and Root Mean Square Error (RMSE) [14]–[20]. Among intelligent methods, PSO is especially preferred for its fast convergence and simple implementation; it has been successfully applied in many disciplines, including direct current motors, robotic manipulators, and intelligent wheelchair systems [21]–[27]. MATLAB/Simulink's modeling accuracy, real-time simulation features, and embedded control system compatibility justified its selection in this study. The 12V DC motor reflects typical actuators found in reasonably priced powered mobility devices.
Recent studies show that PSO-tuned PID controllers in autonomous robots, electric wheelchairs, quadrotor UAVs, and rehabilitation exoskeletons [28]–[30] significantly improve trajectory tracking, rise time, and energy efficiency. Encouraging results have come from hybrid approaches combining PSO with fuzzy logic or neural networks [31]–[35]. Moreover, control strategies for intelligent and adaptive mobility systems such as maximum power point tracking [36], haptic feedback in wheelchairs [37], and adaptive cruise control systems [38] show the adaptability of modern PID techniques.
Prototype development and controller testing for wheelchair systems have been facilitated by simulation tools such as Unity3D and MATLAB/Simulink [39][40]. Modeling research of Mecanum-wheel platforms continues to guide design and controller development [41][42]. However, comparative analyses of PSO and Cohen–Coon tuning methods for PID controllers in Mecanum-based wheelchairs remain limited, especially for low-cost assistive devices.
This study investigates the optimization of four PID controller configurations (P, PI, PD, and PID) using both Cohen–Coon and PSO methods, tested on a second-order electromechanical model of a 12V DC motor designed to emulate real-world actuation in Mecanum-wheel electric wheelchairs [43]–[50]. Time-domain assessments encompassing rise time, settling time, overshoot, and RMSE evaluated the performance of the controller over time. This work is based on a comprehensive evaluation of pertinent literature, including fuzzy-PID [51], neural-PID [52], genetic optimization [53], embedded systems [54]–[56], and assistive robotics [57]–[67].
The main contribution of this work is a systematic, performance-oriented comparison of conventional and intelligent PID tuning procedures, namely Cohen-Coon and PSO, for the management of Mecanum-wheel electric wheelchairs. This study assesses four controller types (P, PI, PD, and PID) utilizing a second-order electromechanical model of a 12V DC motor, illustrating that PSO significantly improves transient and steady-state performance in terms of rise time, settling time, overshoot, and RMSE. The research prioritizes low-cost, embedded mobility platforms, in contrast to most studies focusing on high-end robotic systems, and illustrates that PSO optimization may be effectively executed offline, making it suitable for real-time control in assistive devices. The results not only address the nonlinear and coupled dynamic challenges of Mecanum systems but also provide practical insights for implementing intelligent control strategies in resource-limited applications.
- METHODS
The study concentrated on enhancing PID controller parameters by conventional and intelligent tuning methods through a systematic approach for building, assessing, and analyzing a control system for an electric wheelchair with Mecanum wheels. The research commenced with the creation of mechanical and electronic subsystems, comprising four independently controlled DC motors, an Arduino Due microcontroller, and a joystick-based analog input interface to enable omnidirectional movement.
Second-order electromechanical equations integrating mechanical and electrical dynamics were developed as a mathematical model of the DC motor. The continuous-time model was then discretized for use in digital controllers running in real time.
Two approaches were used to calibrate the PID parameters: PSO, a bio-inspired optimization method that minimizes the Integral of Absolute Error (IAE) by iterative exploration of the parameter space; and the Cohen-Coon method, which evaluates the open-loop step response to ascertain process characteristics including gain and delay.
Closed-loop simulations were utilized to implement each technique across four controller configurations: P, PI, PD, and PID. Rise time, settling time, overshoot, and Integral of Absolute Error (IAE) were employed to evaluate the performance of each controller. The evaluation of these criteria enabled the determination of the ideal configuration in both dynamic and steady-state scenarios.
Fig. 1 depicts the complete PID tuning process, including system modeling, motor parameter identification, controller design, simulation, and performance evaluation.The process begins with identifying the critical parameters that define the dynamic properties of a second-order electromechanical model of the DC motor. The tuning process divides into two concurrent branches. Branch A utilizes process response curves within the conventional analytical framework of the Cohen-Coon approach to assess PID gains. Branch B systematically reduces the Integral of Absolute Error (IAE) using PSO, a bio-inspired metaheuristic technique, to determine optimal gain values. Following a thorough performance evaluation based on critical criteria like IAE, overshoot, and rise time, each branch executes an autonomous PID simulation (Simulation A and Simulation B). The technique culminates in the selection of the ideal controller configuration for use in embedded assistive mobility systems. This structured flowchart distinctly depicts the dual-strategic tuning process utilized in this research.
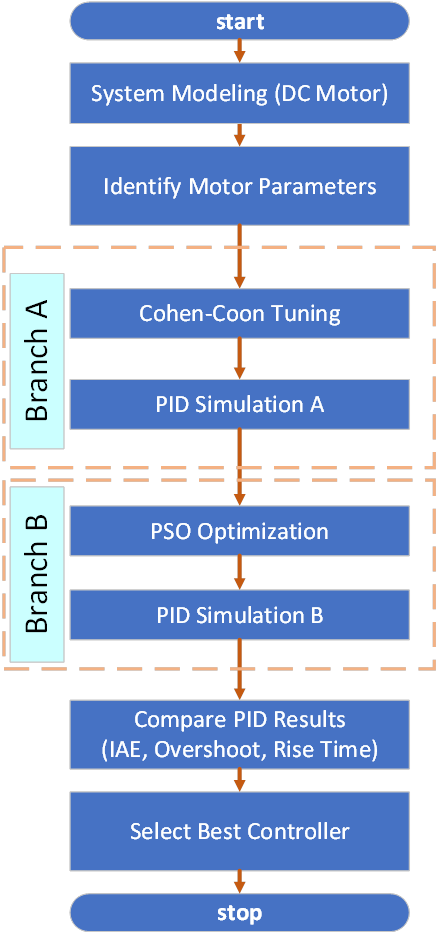
Figure 1. PID Tuning Process Flowchart (Cohen–Coon vs. PSO)
- Design of Electric Cart Control System with Mecanum Wheels
This study delineates the creation of an economical electric wheelchair system, including Mecanum wheels for omnidirectional mobility. The technology is engineered to enable intricate motion in restricted indoor settings, including hospitals, clinics, and residences. The mobility platform is powered by four individually controlled DC motors, each connected to a Mecanum wheel, facilitating movement in forward, backward, lateral, and diagonal directions with fluid transitions. The architecture incorporates analog user input, embedded control, and modular motor drive circuits to facilitate swift and flexible motion control.
Power is provided by a 12 VDC rechargeable battery, linked to a three-position power switch that enables operative, off, and charging modes. A two-axis analog joystick with 10k-ohm potentiometers functions as the input interface, converting user hand movements into analog voltage signals. The Arduino Due microcontroller, chosen for its powerful ARM Cortex-M3 CPU and several ADC channels, processes these data, enabling accurate analog-to-digital conversion and swift processing. PWM signals are generated using the Arduino IDE with standard timer libraries.
Four H-bridge DC motor drivers, each assigned to one of the four motors, control the system outputs. These drivers obtain PWM signals from the microcontroller to independently regulate motor rotation and direction. A safety emergency stop button is incorporated, activating a piezo buzzer through the microcontroller to notify nearby individuals in the occurrence of a hazard or system failure.
The wheelchair's structure is constructed from SUS304L stainless steel, providing mechanical strength and corrosion resistance. The ergonomic design was achieved by cushioned chairs and the strategic positioning of joystick controls on the armrests. The prototype's definitive dimensions are 1,100 mm in length, 560 mm in breadth, and 890 mm in height. These parameters adhere to ISO 2570-2555 standards for powered mobility devices, guaranteeing that the platform fulfills international safety and accessibility criteria can be seen in Table 1. Fig. 2 illustrates the control logic of the system, hardware integration, and wire configuration, highlighting the connection between the power supply, input interface, motor drivers, and microcontroller.
Tabel 1. Comparison of electric wheelchair design dimensions
Dimensions | ISO 2570-2555 requirements (mm) | Designed cart size (mm) |
Overall length | 1,200 | 1,100 |
Overall width | 700 | 560 |
Overall height | 1,090 | 890 |
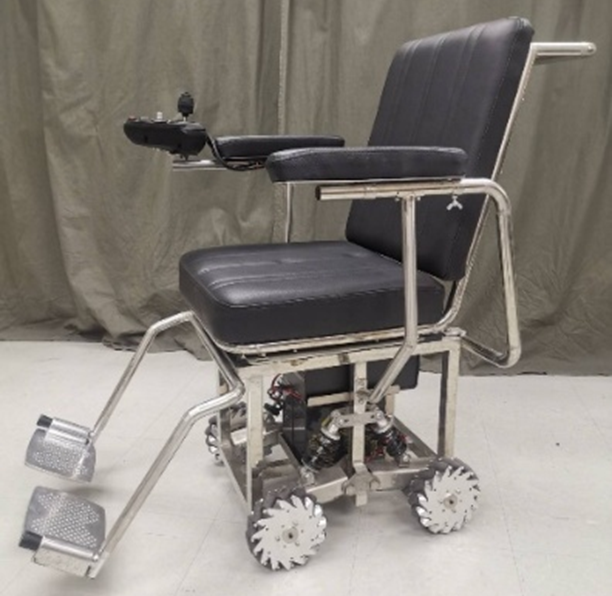
Figure 2. Electric Cart Control System with Mecanum Wheels
- Motor Characterization and Mathematical Modeling
This research used the LX44WG-12-15-527D motor, a brushed DC motor operating at 12 V, equipped with a high-reduction gearbox with a ratio of 1:527. This configuration produces a no-load speed of 15 RPM with a rated torque of around 200 kg·cm, or 19.62 N·m, making it very suitable for low-speed, high-torque applications, such as electric wheelchairs utilizing Mecanum wheels. The compact design and mechanical robustness ensure precise motion control under various load conditions.
A second-order electromechanical model was created to enhance simulation and control design by unifying the electrical and mechanical dynamics of the motor. The modeling commences with the conventional DC motor equations for electrical dynamics in (1), mechanical dynamics in (2), and the linear transfer function in (3).
The equations designate 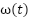 as the rotational velocity,
as the rotational velocity, 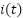 as the armature current, and
as the armature current, and 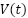 as the applied voltage. Inductance is represented by
as the applied voltage. Inductance is represented by 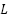 ; resistance by
; resistance by 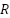 ; back-EMF constant by
; back-EMF constant by 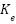 ; torque constant by
; torque constant by 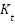 ; rotor inertia by
; rotor inertia by 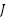 ; and viscous friction coefficient by
; and viscous friction coefficient by 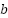 .
.
The torque constant (Kₜ ≈ 2.803 N·m/A) was determined by dividing the rated torque by the anticipated stall current of 7 A. To support this, the back-EMF constant 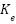 is about 7.38 V·s/rad, calculated by dividing 11.6 by 1.57, and the rotor inertia J is 0.01 kg·m², based on real-world data from similar motors, accounting for the high inertia introduced by the integrated gearbox. The viscous damping coefficient
is about 7.38 V·s/rad, calculated by dividing 11.6 by 1.57, and the rotor inertia J is 0.01 kg·m², based on real-world data from similar motors, accounting for the high inertia introduced by the integrated gearbox. The viscous damping coefficient 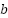 = 0.1 N·m·s was approximated from observation during abrupt motor start-stop behavior instead of being precisely measured. Common datasheet values for such motors provided the resistance and inductance (
= 0.1 N·m·s was approximated from observation during abrupt motor start-stop behavior instead of being precisely measured. Common datasheet values for such motors provided the resistance and inductance (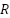 = 0.5 Ω,
= 0.5 Ω, 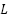 = 0.01 H).
= 0.01 H).
The motor's complete transfer function was obtained by putting these values into (3), therefore illustrating the correlation between the input voltage and the resulting rotational velocity. The continuous-time model was transformed into a discrete-time representation with the Zero-Order Hold (ZOH) method in MATLAB, thereby ensuring compatibility with real-time embedded control systems. The Nyquist criterion guided the selection of a 0.01second sampling interval, which was then validated through time-domain study of the motor's transient behavior. A sampling frequency of 100 Hz is adequate for accurate digital representation and real-time operation on the Arduino platform, given that the primary system dynamics transpire below 20 Hz. The ZOH approach is ideal for discretizing systems with slow electromechanical responses, as it maintains the fundamental dynamic characteristics without causing considerable aliasing or phase distortion. The resultant discrete transfer function was later employed in both the Cohen–Coon and PSO methodologies to calibrate the PID controller in this research.
This model presupposes linear behavior, constant parameters, and minimal influence from noise or temperature fluctuations, which may diverge from real operating conditions. The simulation results validated the mathematical model by closely aligning with experimental motor activity, hence illustrating its relevance for control design. Fig. 3 illustrates the compact, gearbox-integrated motor assembly used to transmit torque to the Mecanum wheels, emphasizing the motor’s physical configuration.

Figure 3. DC Motor Used in the Mecanum Wheel System
- System Design
This project uses a closed-loop feedback control system with a Proportional–Integral–Derivative (PID) controller to manage the motor speed of the Mecanum-wheel platform. The PID control framework is a prominent method in industrial and robotic control, recognized for its structural simplicity, ease of implementation, and ability to deliver robust performance across many dynamic systems. Fig. 4 shows the basic setup of the closed-loop system, where the controller continuously adjusts the control signal 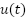 based on the gap between the target output
based on the gap between the target output 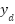 and the actual output
and the actual output 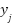 , generating the error signal
, generating the error signal 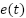 .
.
The PID controller has three key parts: a proportional term that addresses the current error magnitude, an integral term that accumulates past errors to eliminate steady-state offsets, and a derivative term that predicts future errors based on the rate of change. This design optimizes stability and minimizes overshoot, thereby allowing the system to respond rapidly to external disturbances.
The continuous-time control law is mathematically expressed as follows.
| 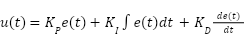
| (4) |
Where 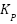 ,
, 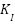 , and
, and 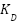 represent the proportional, integral, and derivative gains, respectively. This formulation is frequently employed in theoretical analysis and simulation research. For practical application on digital controllers or microcontroller-based devices such as the Arduino Due, this equation must be discretized to enable time-sampled computation. Techniques such as numerical integration and differentiation facilitate the development of a discrete version, which can subsequently be implemented in embedded software written in C/C++.
represent the proportional, integral, and derivative gains, respectively. This formulation is frequently employed in theoretical analysis and simulation research. For practical application on digital controllers or microcontroller-based devices such as the Arduino Due, this equation must be discretized to enable time-sampled computation. Techniques such as numerical integration and differentiation facilitate the development of a discrete version, which can subsequently be implemented in embedded software written in C/C++.
PID was chosen over more intricate systems (e.g., fuzzy logic or model predictive control) due to its simplicity in implementation and effectiveness in low-cost embedded applications. Moreover, the controller's capacity for fine-tuning through several techniques, such as Cohen–Coon or PSO, renders it particularly suitable for mobile robots necessitating accurate trajectory control and real-time stability.
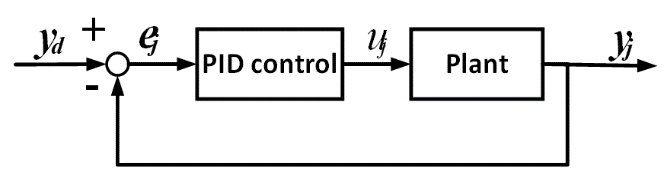
Figure 4. Block Diagram of the PID Control System
- Cohen-Coon Tuning
Cohen-Coon tuning is a classic method used to find the best settings for proportional-integral-derivative (PID) controllers by looking at how the process responds over time. It works particularly well for first-order systems that have a delay and is commonly used when the system can be described by a first-order plus time-delay (FOPTD) model. This method improves stability and performance relative to the Ziegler-Nichols approach by explicitly accounting for both delay times and time constants.
The Cohen-Coon tuning method involves applying a step input to the system and analyzing its open-loop step response. From the process response curve (shown in Fig. 5), two pivotal times are discerned: 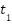 denotes the moment when the output attains 28.3% of the steady-state value, while
denotes the moment when the output attains 28.3% of the steady-state value, while 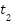 signifies the time when it reaches 63.2% of the steady-state value 𝑦𝑠𝑠. The following points are utilized to calculate the system time constant
signifies the time when it reaches 63.2% of the steady-state value 𝑦𝑠𝑠. The following points are utilized to calculate the system time constant 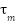 and the time delay
and the time delay 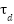 .
.
| 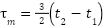
| (5) |
| 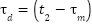
| (6) |
Once 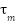 ,
, 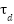 , and the process gain
, and the process gain 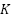 are determined, the Cohen-Coon equations are used to find the PID gains for various controller setups. The complete formulas are presented in Table 2.
are determined, the Cohen-Coon equations are used to find the PID gains for various controller setups. The complete formulas are presented in Table 2.
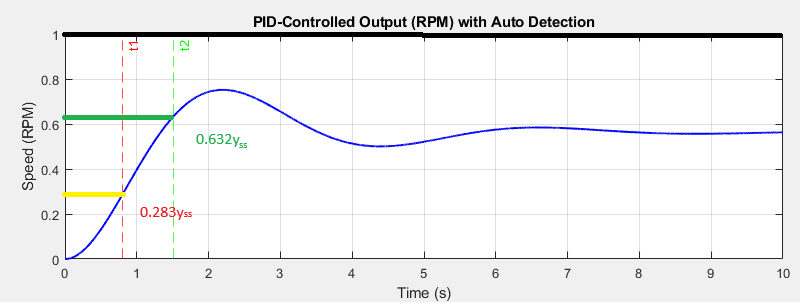
Figure 5. Process reaction curve used to extract 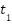 and
and 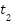
This study entailed the programmed computation of Cohen-Coon parameters using MATLAB. The plant model created in the system identification phase was used to simulate the open-loop step response, which helped find the values of 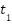 and
and 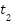 . The computed time constant and delay time were later included into the previously discussed equations to derive the final controller gains. The technique was repeated for each of the four controller types: P, PI, PD, and PID.
. The computed time constant and delay time were later included into the previously discussed equations to derive the final controller gains. The technique was repeated for each of the four controller types: P, PI, PD, and PID.
The Cohen-Coon method provides a simple and effective way to set PID parameters, especially useful for systems like electric wheelchairs that have delays and slow responses. However, as demonstrated in the Results section, fine-tuning using metaheuristic techniques such as Particle Swarm Optimization may significantly enhance both transient and steady-state performance.
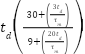
Table 3 shows the step-by-step instructions for adjusting a PID controller using the Cohen-Coon method, which is specifically made for a DC motor in an electric wheelchair system. The procedure starts with the initialization of essential motor and simulation parameters, followed by modeling the motor in both continuous and discrete domains. A basic simulation is done to find important step response features, specifically the times when the system reaches 28.3% and 63.2% of its final value. These are employed to compute the process gain, time constant (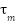 ), and delay (
), and delay (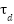 ). The Cohen-Coon tuning formulae are utilized to ascertain PID gains for each control configuration (P, PI, PD, PID). Each configuration is simulated autonomously, and its performance is evaluated utilizing the Integral of Absolute Error (IAE). The setup that produces the minimal IAE is deemed best, with data shown and documented for examination.
). The Cohen-Coon tuning formulae are utilized to ascertain PID gains for each control configuration (P, PI, PD, PID). Each configuration is simulated autonomously, and its performance is evaluated utilizing the Integral of Absolute Error (IAE). The setup that produces the minimal IAE is deemed best, with data shown and documented for examination.
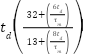
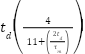
Table 2. Cohen-Coon tuning formula [43]
Type of Controller | 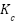
| 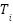
| 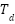
|
P | 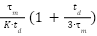
| - | - |
PI | 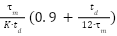
| 
| - |
PD | 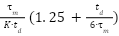
| - | 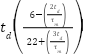
|
PID | 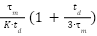
| 
| 
|
Table 3. Cohen–Coon-Based PID Tuning Workflow
Step | Description |
1 | Initialize motor model parameters |
2 | Build the transfer function using Equation (3) |
3 | Simulate the open-loop step response |
4 | Extract 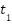 and and 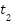 |
5 | Compute 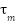 and and 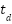 |
6 | Use Cohen–Coon formulas to determine PID gains |
7 | Simulate closed-loop responses for P, PI, PD, PID |
8 | Compute IAE and select configuration with lowest IAE |
2.4. Particle Swarm Optimization (PSO)
Particle swarm optimization (PSO) is a population-based optimization technique that is motivated by the coordinated movements of fish and birds. This study utilizes PSO to reduce the control error between the system output and the reference input, thereby improving the performance of a variety of PID controller configurations, including Proportional (P), Proportional-Integral (PI), Proportional-Derivative (PD), and Proportional-Integral-Derivative (PID). Since it quantifies the output deviation from the target value throughout the entire simulation period, the integral of absolute error (IAE) is chosen as the objective for this optimization. It is stated that the IAE is mathematically formulated as
| 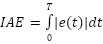
| (7) |
In this context, 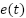 represents the instantaneous error, while T specifies the entire simulation duration, which is 10 seconds for the purposes of this analysis.
represents the instantaneous error, while T specifies the entire simulation duration, which is 10 seconds for the purposes of this analysis.
The optimization process was conducted using the MATLAB built-in function ‘particleswarm()’, with a maximum of 50 iterations and a swarm size of 30 particles. The search space of each controller type was distinct, as it was defined by specific lower and upper PID gain ranges. The P controller employs a single parameter (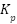 ) restricted to the interval [0.1, 20], while the PID controller employs three parameters (
) restricted to the interval [0.1, 20], while the PID controller employs three parameters (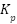 ,
, 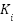 ,
, 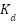 ) with respective ranges of [0.1, 0.01, 0.0001] and [10, 100, 10]. Reliable performance and optimization flexibility were guaranteed by these characteristics.
) with respective ranges of [0.1, 0.01, 0.0001] and [10, 100, 10]. Reliable performance and optimization flexibility were guaranteed by these characteristics.
The chosen gain limits ensure the feasibility of control and accurately depict the dynamics of the actuator. Under-actuation is prevented by a minimum threshold of 0.1, while excessive energy consumption, control signal oscillation, or actuator saturation are avoided by a maximum threshold of 20. These limitations are consistent with the control methodologies that have been previously documented for brushed DC motors in mobile robotics. 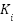 and
and 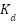 implemented practical categories that were analogous in nature and based on proportional relationships that were calibrated by literature norms and preparatory testing.
implemented practical categories that were analogous in nature and based on proportional relationships that were calibrated by literature norms and preparatory testing.
The empirical determination of a swarm size of 30 and an iteration count of 50 was facilitated by established methodologies in analogous PSO-based control applications, thereby optimizing the balance between convergence quality and computational expenditure. The initial simulations indicated that these parameters were sufficient to achieve consistent and reproducible convergence. Although no formal sensitivity analysis was performed, numerous studies have confirmed a consistent decrease in the IAE objective across a variety of random seeds.
The determination of gain search ranges was facilitated by the physical system's constraints and antecedent control design knowledge. The traditional ratios observed in stable PID designs for electromechanical systems were used to determine 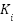 and
and 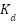 . However,
. However, 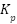 was restricted to a range of 0.1 to 20 to prevent actuator saturation and guarantee a realistic dynamic response. This limited the optimizer to analyzing gain regions that were stable and practically feasible.
was restricted to a range of 0.1 to 20 to prevent actuator saturation and guarantee a realistic dynamic response. This limited the optimizer to analyzing gain regions that were stable and practically feasible.
The optimization procedure was conducted independently for each controller type. The standard PID control formula was employed to apply the PID gains for each particle, or solution candidate, in a discrete-time simulation of the DC motor system. The discrete PID's operational control law is denoted by (4).
The IAE provided the cost criterion to evaluate and rank the performance of each particle after calculating the output response. The optimal solution for the set of gains was identified and implemented in subsequent simulations upon convergence. This approach enabled the automated and efficient adjustment of PID controllers, eliminating the need for manual modifications or analytical models. As a result, a specific set of gain configurations produces optimal tracking performance for all controller types, regardless of motor behavior and real-world complexities.
The pseudo-code format of the exhaustive PSO-based tuning procedure is summarized in Table 4. This work outlines the process for configuring motor settings, modifying controller parameters, performing PSO optimization, modeling system responses in a closed loop, and selecting the minimal IAE controller. This approach guarantees the uniform and equitable calibration of all controller types, thereby establishing a strong foundation for performance evaluation across configurations.
Table 4. PSO-Based PID Optimization Workflow
Step | Description |
1 | Configure motor and simulation settings |
2 | Develop the motor transfer function and transform it into a discrete model. |
3 | Configure controller settings (P, PI, PD, PID) |
4 | Optimize controller parameters via Particle Swarm Optimization. |
- Define cost function (IAE) |
- Run PSO to minimize cost |
- Save optimal gains |
5 | Simulate system response with optimized gains |
- Apply PID formula in loop |
- Compute error and PID terms |
- Saturate and apply control |
6 | Plot all controller responses |
7 | Identify best controller based on IAE |
- RESULT AND DISCUSSION
This section compares two PID tuning methodologies: Cohen-Coon, a conventional technique, and PSO, a metaheuristic approach, with respect to system control performance. The objective is to assess the enhancement of transient and steady-state responses of a Mecanum-wheel electric wheelchair system under a 15 RPM step input for each technique.
- Motor Step Response Characterization
Fig. 6 illustrates the simulated step response of the LX44WG-12-15-527D DC motor under a constant 12V input. The solid blue line represents the motor's output speed in RPM, while the red dashed line indicates the control voltage. Prior to stabilizing at the objective of 15 RPM, the motor exhibits a peak overshoot of around 18 RPM, representing a 20% deviation. This behavior illustrates an underdamped second-order system, marked by a swift rise time, moderate overshoot, and acceptable settling characteristics.
This response profile corresponds with expected behavior for motors exhibiting significant gear reduction, where inertia and limited damping result in abrupt overshoot. The study omitted hardware testing; however, the simulated dynamics correspond with previously documented performance in experimental analyses of analogous brushed DC motors under substantial mechanical stress.
The simulation-based characterization provides a reliable, consistent, and cost-effective framework for evaluating controller performance under standardized conditions. It enables the progressive refinement of control methodologies while mitigating hardware risk. Moreover, accurate modeling of real-world transient dynamics in simulations aids in the creation of controllers aimed at reducing overshoot and improving settling time, both crucial for mobility applications that need smooth and safe movement.
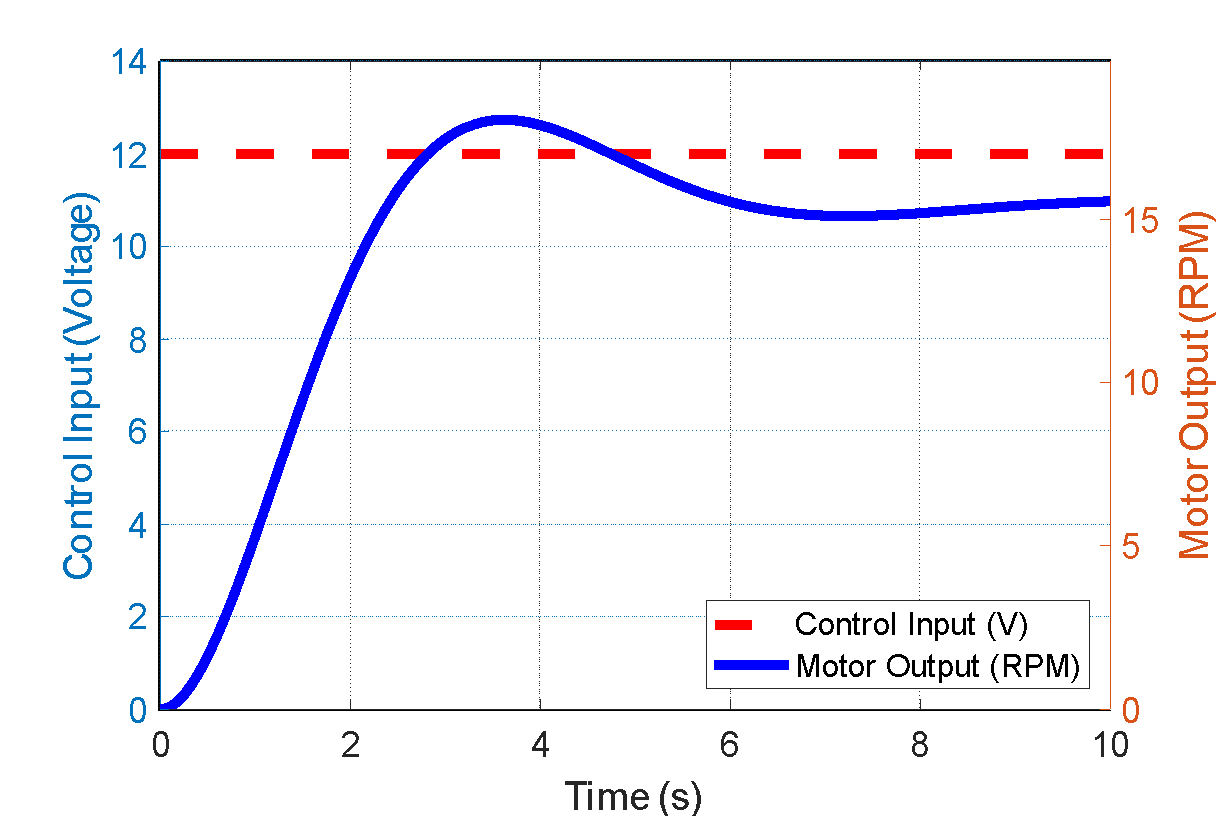
Figure 6. Motor Output in RPM for 12V Step Input
3.2. Controller Performance Comparison
To assess the effectiveness of various control systems, four types of controllers: Proportional (P), Proportional-Integral (PI), Proportional-Derivative (PD), and Proportional-Integral-Derivative (PID), were deployed and evaluated under uniform conditions. Each controller was automatically adjusted using two different methods: the classic Cohen-Coon technique and the PSO algorithm. The system received a 12V step input, and the motor's dynamic reactions were examined in the time domain.
The precise gain values employed in this study for each controller configuration were ascertained utilizing both the Cohen-Coon and PSO methodologies. In the Cohen-Coon methodology, the proportional controller utilized a proportional gain (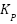 ) of 2.0583. The PI controller utilized a proportional gain (
) of 2.0583. The PI controller utilized a proportional gain (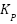 ) of 1.6791 and an integral gain (
) of 1.6791 and an integral gain (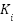 ) of 1.9175. The PD controller's proportional and derivative gains were
) of 1.9175. The PD controller's proportional and derivative gains were 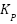 = 2.3729 and
= 2.3729 and 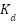 = 0.2601, respectively. The whole PID controller employed gains of
= 0.2601, respectively. The whole PID controller employed gains of 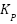 = 2.0583,
= 2.0583, 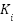 = 1.9633, and
= 1.9633, and 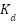 = 0.3468. The PSO-based tuning approach yielded more aggressive and optimized settings. The P controller was calibrated with
= 0.3468. The PSO-based tuning approach yielded more aggressive and optimized settings. The P controller was calibrated with 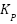 = 20.0000, whereas the PI setup employed
= 20.0000, whereas the PI setup employed 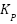 = 10.0000 and
= 10.0000 and 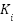 = 0.6136. The PSO determined optimal settings for the PD controller as
= 0.6136. The PSO determined optimal settings for the PD controller as 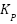 = 10.0000 and
= 10.0000 and 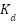 = 1.9544. The PID controller optimized by PSO was assigned gain values of
= 1.9544. The PID controller optimized by PSO was assigned gain values of 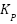 = 9.8790,
= 9.8790, 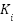 = 0.6125, and
= 0.6125, and 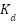 = 3.5501. These numbers show how well the PSO algorithm can adjust settings to find the best gain combinations that reduce the Integral of Absolute Error (IAE) and enhance the system's performance.
= 3.5501. These numbers show how well the PSO algorithm can adjust settings to find the best gain combinations that reduce the Integral of Absolute Error (IAE) and enhance the system's performance.
Fig. 7 illustrates the response curves for all configurations, revealing differences in rise time, settling time, overshoot, and steady-state accuracy. Controllers optimized via PSO demonstrated faster, more stable, and more accurate responses compared to those tuned with Cohen–Coon.
Table 5 presents a quantitative comparison of control performance. This table comprises essential time-domain measurements, including rising time, settling time, overshoot percentage, and Root Mean Square Error (RMSE). Among these measures, RMSE functions as the primary measure of total control accuracy. The chart shows that the PID controller improved by PSO performed the best in all four measures, emphasizing how well intelligent optimization methods work in complex and sensitive situations like Mecanum-wheeled mobility systems.
The results clearly indicate that PSO-tuned controllers outperform their Cohen–Coon counterparts in nearly every aspect. The PSO-tuned PID controller achieved the lowest RMSE (4.59), fastest settling time (2.37 s), and minimal overshoot (0.78%), making it especially suitable for precise mobility-assistive applications. In contrast, while Cohen–Coon controllers exhibit commendable performance under standard conditions, they reveal significantly increased overshoot and prolonged settling times, particularly in the PI and PID configurations. An overshoot surpassing 20% in the PID-Cohen–Coon arrangement may result in user frustration or instability in control during practical application. Overall, PSO demonstrates efficacy in optimizing Proportional-Integral-Derivative (PID) controllers for nonlinear systems, including Mecanum-wheel electric wheelchairs. Its ability to operate without linear model assumptions makes it very appropriate for intelligent embedded control systems.
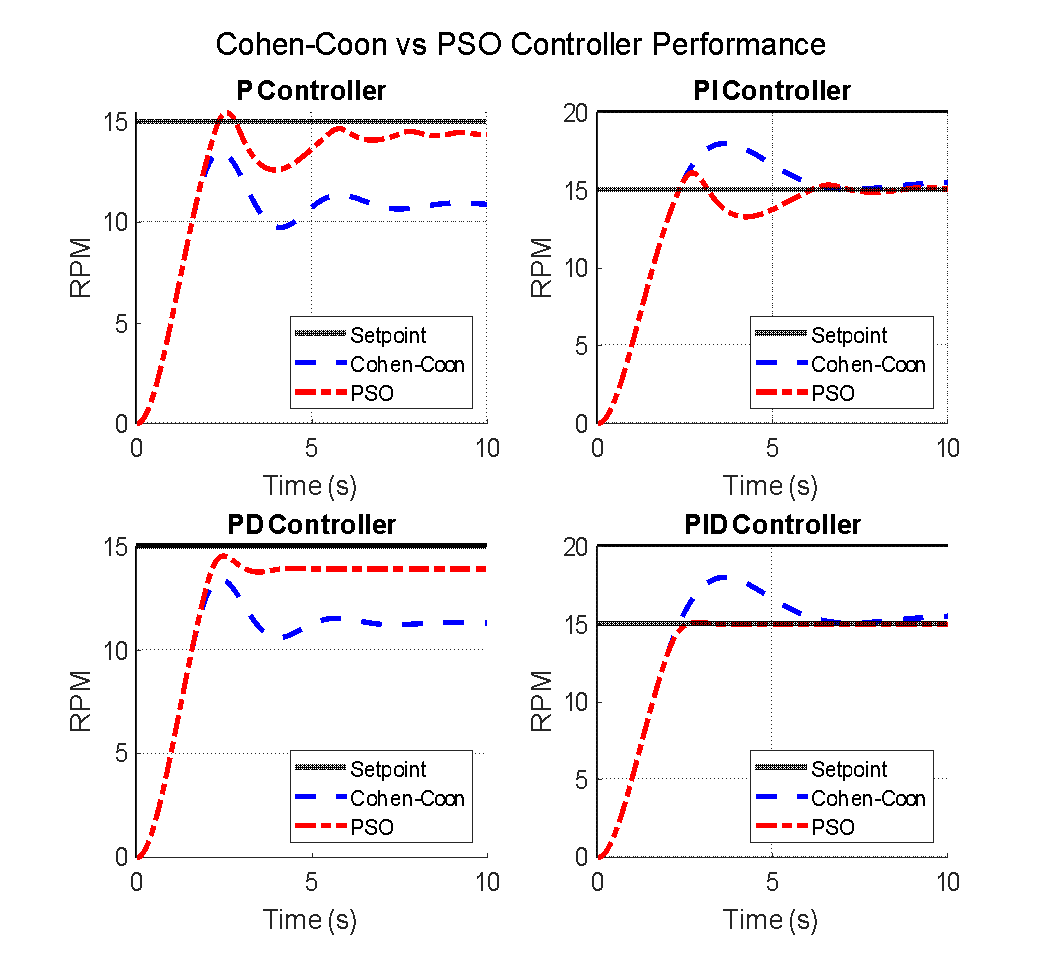
Figure 7. Comparison of Cohen-Coon vs PSO Controller Performance
Table 5. Performance Metrics Comparison between Cohen-Coon and PSO Tuning Methods
Controller Type | Tuning Method | Rise Time (s) | Settling Time (s) | Overshoot (%) | RMSE |
P | Cohen-Coon | 2.306 | 5.645 | -9.75% | 5.8110 |
P | PSO | 2.052 | 5.771 | 3.20% | 4.6916 |
PI | Cohen-Coon | 2.052 | 5.822 | 20.14% | 4.7655 |
PI | PSO | 2.052 | 5.704 | 7.51% | 4.6349 |
PD | Cohen-Coon | 2.416 | 5.033 | -10.55% | 5.5900 |
PD | PSO | 2.060 | 4.112 | -3.03% | 4.6780 |
PID | Cohen-Coon | 2.052 | 6.119 | 20.14% | 4.7655 |
PID | PSO | 2.058 | 2.365 | 0.78% | 4.5850 |
- Analysis, Interpretation, and Practical Implications
The comparison research demonstrated a consistent trend among all controller types: controllers optimized by PSO surpassed those optimized using the conventional Cohen–Coon method in both transient and steady-state performance. The PSO-based optimization for P, PI, PD, and PID configurations resulted in expedited rise times, diminished settling times, decreased overshoot percentages, and lower root mean square error (RMSE) values.
The Cohen–Coon-tuned PID controller necessitated 6.12 seconds to reach stability, while the PSO-tuned PID controller achieved a rise time of approximately 2.06 seconds and a settling time of 2.37 seconds. Overshoot was markedly diminished, from 20.14% to 0.78%, utilizing PSO. These enhancements signify enhanced functionality and increased safety, which are essential for assistive mobility devices necessitating comfort and precision. Moreover, reduced RMSE values in PSO designs indicate superior tracking precision under fluctuating operational situations.
Systems utilizing Mecanum wheels frequently demonstrate intricate multi-directional forces and fluctuating payloads, rendering conventional tuning techniques inadequate. The Cohen–Coon technique, based on linear, time-invariant assumptions, may be inadequate in nonlinear and dynamic contexts. Conversely, PSO investigates a wider solution space through swarm intelligence, identifying globally optimal gain sets that adapt to these dynamic conditions.
The results align with the observations of Isdaryani et al. [43], who determined that while Cohen–Coon tuning enhanced performance compared to Ziegler–Nichols in magnetic levitation systems, it did not provide the robustness necessary for highly dynamic applications. Our research corroborates this by illustrating that PSO provides substantial benefits, especially in embedded control systems necessitating real-time responsiveness and stability.
Despite PSO necessitating greater processing resources during the optimization phase, this process is performed offline. Once the optimal gain values are identified, they can be directly programmed into microcontrollers without additional real-time processing overhead. This renders PSO especially appropriate for resource-limited embedded applications, such as electric wheelchairs.
Despite these advantages, certain limits must be recognized. The evaluations were performed exclusively in a virtual setting. While previous experiments guided the modeling methodology, the simulations omitted real-world variables such as sensor noise, actuator nonlinearities, and mechanical deterioration. The effectiveness of PSO depends on initialization factors; the swarm size (30) and iteration count (50) used in this study were chosen empirically and may not be suitable for other platforms.
In conclusion, PSO offers a resilient, adaptable, and efficient substitute for traditional PID tuning techniques, particularly for intricate mobility-assistive systems characterized by nonlinear dynamics and fluctuating loads. Although classical methods such as Cohen–Coon are valuable for preliminary estimations, advanced optimization algorithms like PSO are more adept at fulfilling contemporary requirements for precision, dependability, and safety in practical applications.
- CONCLUSIONS
This research evaluated two PID tuning methodologies, PSO and Cohen–Coon, for a Mecanum-wheel electric wheelchair system. Four controller configurations (P, PI, PD, and PID) were simulated under conditions of step input tracking. PSO significantly surpassed Cohen–Coon regarding rise time, settling time, overshoot, and root mean square error (RMSE). The PSO-tuned PID configuration demonstrated optimal performance among all controllers, with a rise time of approximately 2.06 seconds, a settling time of 2.37 seconds, an overshoot of 0.78%, and an RMSE of 4.59. These results substantiate the efficacy of PSO in determining the optimal gain settings while taking into account the nonlinear dynamics that are inherent to omnidirectional mobility platforms. The optimization process occurs offline, eliminating the need for real-time calculation and rendering the use of PSO in embedded microcontroller systems viable. This research advances the area by illustrating the effective utilization of PSO in calibrating control systems for electric wheelchairs, where accuracy, stability, and user comfort are paramount. Nevertheless, this study has certain limitations. All assessments were performed in a simulated environment without hardware verification. Real-world variables, including ambient disturbances, actuator saturation, and sensor noise, were excluded from the models. Additionally, the swarm size and starting parameters were established empirically, potentially affecting the performance of PSO in various conditions. Subsequent research should incorporate experimental validation through physical systems to ascertain the practical efficacy of the proposed methodology. Comparative assessments utilizing various metaheuristic algorithms, such as differential evolution or genetic algorithms, may yield enhanced insights into tuning robustness. Further research should assess the effects of PSO-derived aggressive gain settings on energy consumption, actuator degradation, and long-term stability. In summary, PSO offers a feasible and scalable substitute for traditional PID tuning methods in assistive mobility systems. Its capacity to optimize controller parameters in dynamic and uncertain environments renders it especially appropriate for real-time embedded control applications.
ACKNOWLEDGEMENT
The researcher acknowledges the financial assistance the research team received from the research institute, academic services center, and college of biomedical engineering at Rangsit University. The Ethics Review Board of Rangsit University has evaluated the study, reference number RSUERB2025-006, and confirmed that the research does not involve human subjects. Moreover, AI-driven methods (QuillBot Premium) were utilized for grammatical verification, paraphrasing, and linguistic augmentation to ensure the accuracy and clarity of the text.
REFERENCES
- N. Thongpance and P. Chotikunnan, “Design and Construction of Electric Wheelchair with Mecanum Wheel,” Journal of Robotics and Control (JRC), vol. 4, no. 1, pp. 71–82, 2023, https://doi.org/10.18196/jrc.v4i1.17095.
- P. S. Yadav, V. Agrawal, J. C. Mohanta, and M. F. Ahmed, “A robust sliding mode control of Mecanum wheel-chair for trajectory tracking,” Materials Today: Proceedings, vol. 56, pp. 623–630, 2022, https://doi.org/10.1016/j.matpr.2021.12.398.
- Z. Yuan, Y. Tian, Y. Yin, S. Wang, J. Liu, and L. Wu, “Trajectory tracking control of a four Mecanum wheeled mobile platform: An extended state observer‐based sliding mode approach,” IET Control Theory & Applications, vol. 14, no. 3, pp. 415–426, 2020, https://doi.org/10.1049/iet-cta.2018.6127.
- J. Palacín, D. Martínez, E. Rubies, and E. Clotet, “Suboptimal omnidirectional wheel design and implementation,” Sensors, vol. 21, no. 3, p. 865, 2021, https://doi.org/10.3390/s21030865.
- C. Kim, J. Suh, and J. H. Han, “Development of a hybrid path planning algorithm and a bio-inspired control for an omni-wheel mobile robot,” Sensors, vol. 20, no. 15, p. 4258, 2020, https://doi.org/10.3390/s20154258.
- A. Ma'arif and N. R. Setiawan, “Control of DC motor using integral state feedback and comparison with PID: Simulation and Arduino implementation,” Journal of Robotics and Control (JRC), vol. 2, no. 5, pp. 456–461, 2021, https://doi.org/10.18196/jrc.25122.
- E. S. Rahayu, A. Ma'arif, and A. Cakan, “Particle swarm optimization (PSO) tuning of PID control on DC motor,” International Journal of Robotics and Control Systems, vol. 2, no. 2, pp. 435–447, 2022, https://doi.org/10.31763/ijrcs.v2i2.476.
- M. Samuel, M. Mohamad, M. Hussein, and S. M. Saad, “Lane keeping maneuvers using proportional integral derivative (PID) and model predictive control (MPC),” Journal of Robotics and Control (JRC), vol. 2, no. 2, pp. 78–82, 2021, https://doi.org/10.18196/jrc.2256.
- Z. Dachang, D. Baolin, Z. Puchen, and C. Shouyan, “Constant force PID control for robotic manipulator based on fuzzy neural network algorithm,” Complexity, vol. 2020, no. 1, p. 3491845, 2020, https://doi.org/10.1155/2020/3491845.
- G. B. So, “A modified 2-DOF control framework and GA-based intelligent tuning of PID controllers,” Processes, vol. 9, no. 3, p. 423, 2021, https://doi.org/10.3390/pr9030423.
- S. Mahfoud, A. Derouich, N. El Ouanjli, M. El Mahfoud, and M. Taoussi, “A new strategy-based PID controller optimized by genetic algorithm for DTC of the doubly fed induction motor,” Systems, vol. 9, no. 2, p. 37, 2021, https://doi.org/10.3390/systems9020037.
- Q. Huang et al., “An EOG-based human–machine interface for wheelchair control,” IEEE Transactions on Biomedical Engineering, vol. 65, no. 9, pp. 2023–2032, 2017, https://doi.org/10.1109/TBME.2017.2732479.
- Z. Qi, Q. Shi, and H. Zhang, “Tuning of digital PID controllers using particle swarm optimization algorithm for a CAN-based DC motor subject to stochastic delays,” IEEE Transactions on Industrial Electronics, vol. 67, no. 7, pp. 5637–5646, 2019, https://doi.org/10.1109/TIE.2019.2934030.
- A. L. Shuraiji and S. W. Shneen, “Fuzzy logic control and PID controller for brushless permanent magnetic direct current motor: A comparative study,” Journal of Robotics and Control (JRC), vol. 3, no. 6, pp. 762–768, 2022, https://doi.org/10.18196/jrc.v3i6.15974.
- A. S. Mohammed, T. H. Sikiru, I. Bello, A. T. Salawudeen, and U. A. Dodo, “Modified fractional order PID controller for load frequency control of four area thermal power system,” International Journal of Robotics & Control Systems, vol. 3, no. 2, 2023, https://doi.org/10.31763/ijrcs.v3i2.957.
- M. Mukhtar, D. Khudher, and T. Kalganova, “A control structure for ambidextrous robot arm based on multiple adaptive neuro‐fuzzy inference system,” IET Control Theory & Applications, vol. 15, no. 11, pp. 1518–1532, 2021, https://doi.org/10.1049/cth2.12140.
- Y. Chen, B. Chu, and C. T. Freeman, “Iterative learning control for robotic path following with trial-varying motion profiles,” IEEE/ASME Transactions on Mechatronics, vol. 27, no. 6, pp. 4697–4706, 2022, https://doi.org/10.1109/TMECH.2022.3164101.
- P. Chotikunnan, R. Chotikunnan, A. Nirapai, A. Wongkamhang, P. Imura, and M. Sangworasil, “Optimizing membership function tuning for fuzzy control of robotic manipulators using PID-driven data techniques,” Journal of Robotics and Control (JRC), vol. 4, no. 2, pp. 128–140, 2023, https://doi.org/10.18196/jrc.v4i2.18108.
- J. Han, F. Wang, and C. Sun, “Trajectory tracking control of a manipulator based on an adaptive neuro-fuzzy inference system,” Applied Sciences, vol. 13, no. 2, p. 1046, 2023, https://doi.org/10.3390/app13021046.
- D. A. Pham and S. H. Han, “Enhancing underwater robot manipulators with a hybrid sliding mode controller and neural-fuzzy algorithm,” Journal of Marine Science and Engineering, vol. 11, no. 12, p. 2312, 2023, https://doi.org/10.3390/jmse11122312.
- R. S. Patil, S. P. Jadhav, and M. D. Patil, “Review of intelligent and nature-inspired algorithms-based methods for tuning PID controllers in industrial applications,” Journal of Robotics and Control (JRC), vol. 5, no. 2, pp. 336–358, 2024, https://doi.org/10.18196/jrc.v5i2.20850.
- P. Chotikunnan, W. Khotakham, A. Wongkamhang, A. Nirapai, P. Imura, K. Roongpraser, R. Chotikunnan, and N. Thongpance, “Genetic algorithm-optimized LQR for enhanced stability in self-balancing wheelchair systems,” Control Systems and Optimization Letters, vol. 2, no. 3, pp. 327–335, 2024, https://doi.org/10.59247/csol.v2i3.161.
- H. Zhang, Z. Zhao, Y. Wei, Y. Liu, and W. Wu, “A self-tuning variable universe fuzzy PID control framework with hybrid BAS-PSO-SA optimization for unmanned surface vehicles,” Journal of Marine Science and Engineering, vol. 13, no. 3, p. 558, 2025, https://doi.org/10.3390/jmse13030558.
- M. M. Nishat, F. Faisal, A. J. Evan, M. M. Rahaman, M. S. Sifat, and H. F. Rabbi, “Development of genetic algorithm (GA) based optimized PID controller for stability analysis of DC-DC buck converter,” Journal of Power and Energy Engineering, vol. 8, no. 9, p. 8, 2020, https://doi.org/10.4236/jpee.2020.89002.
- R. Kristiyono and W. Wiyono, “Autotuning fuzzy PID controller for speed control of BLDC motor,” Journal of Robotics and Control (JRC), vol. 2, no. 5, pp. 400–407, 2021, https://doi.org/10.18196/jrc.25114.
- Z. Qu, W. Younis, X. Liu, A. K. Junejo, S. Z. Almutairi, and P. Wang, “Optimized PID controller for load frequency control in multi-source and dual-area power systems using PSO and GA algorithms,” IEEE Access, 2024, https://doi.org/10.1109/ACCESS.2024.3445165.
- M. S. Gharajeh and H. B. Jond, “Hybrid global positioning system-adaptive neuro-fuzzy inference system based autonomous mobile robot navigation,” Robotics and Autonomous Systems, vol. 134, p. 103669, 2020, https://doi.org/10.1016/j.robot.2020.103669.
- A. K. Hado, B. S. Bashar, M. M. A. Zahra, R. Alayi, Y. Ebazadeh, and I. Suwarno, “Investigating and optimizing the operation of microgrids with intelligent algorithms,” Journal of Robotics and Control (JRC), vol. 3, no. 3, pp. 279–288, 2022, https://doi.org/10.18196/jrc.v3i3.14772.
- M. Kiew-ong-art, P. Chotikunnan, A. Wongkamhang, R. Chotikunnan, A. Nirapai, P. Imura, M. Sangworasil, N. Thongpance, and A. Srisiriwat, “Comparative study of Takagi-Sugeno-Kang and Madani algorithms in Type-1 and Interval Type-2 fuzzy control for self-balancing wheelchairs,” International Journal of Robotics and Control Systems, vol. 3, no. 4, pp. 643–657, 2023, https://doi.org/10.31763/ijrcs.v3i4.1154.
- M. Rinaldi, M. Moslehi, G. Guglieri, and S. Primatesta, “PSO-based PID tuning for PMSM-quadrotor UAV system,” Engineering Proceedings, vol. 90, no. 1, p. 2, 2025, https://doi.org/10.3390/engproc2025090002.
- M. A. Abdelghany, A. O. Elnady, and S. O. Ibrahim, “Optimum PID controller with fuzzy self-tuning for DC servo motor,” Journal of Robotics and Control (JRC), vol. 4, no. 4, pp. 500–508, 2023, https://doi.org/10.18196/jrc.v4i4.18676.
- Z. Wang, L. Zou, X. Su, G. Luo, R. Li, and Y. Huang, “Hybrid force/position control in workspace of robotic manipulator in uncertain environments based on adaptive fuzzy control,” Robotics and Autonomous Systems, vol. 145, p. 103870, 2021, https://doi.org/10.1016/j.robot.2021.103870.
- T. A. Lin, Y. C. Lee, W. J. Chang, and Y. H. Lin, “Robust observer-based proportional derivative fuzzy control approach for discrete-time nonlinear descriptor systems with transient response requirements,” Processes, vol. 12, no. 3, p. 540, 2024, https://doi.org/10.3390/pr12030540.
- B. Ramesh and K. Lakshmanna, “A novel early detection and prevention of coronary heart disease framework using hybrid deep learning model and neural fuzzy inference system,” IEEE Access, vol. 12, pp. 26683–26695, 2024, https://doi.org/10.1109/ACCESS.2024.3366537.
- M. Singh, S. Arora, and O. A. Shah, “Enhancing hybrid power system performance with GWO-tuned fuzzy-PID controllers: A comparative study,” International Journal of Robotics & Control Systems, vol. 4, no. 2, 2024, https://doi.org/10.31763/ijrcs.v4i2.1388.
- M. A. Azad, A. Sarwar, M. Tariq, F. I. Bakhsh, S. Ahmad, A. S. N. Mohamed, and M. R. Islam, “Global maximum power point tracking for photovoltaic systems under partial and complex shading conditions using a PID based search algorithm (PSA),” IET Renewable Power Generation, vol. 19, no. 1, p. e70005, 2025, https://doi.org/10.1049/rpg2.70005.
- M. A. Hadj-Abdelkader, G. Bourhis, and B. Cherki, “Haptic feedback control of a smart wheelchair,” Applied Bionics and Biomechanics, vol. 9, no. 2, pp. 181–192, 2012, https://doi.org/10.1155/2012/921982.
- V. Chaurasia, A. N. Tiwari, and S. M. Tripathi, “Optimal hybrid strategy in adaptive cruise control system for enhanced autonomous vehicle stability and safety,” Computers and Electrical Engineering, vol. 118, p. 109377, 2024, https://doi.org/10.1016/j.compeleceng.2024.109377.
- Y. Morere, G. Bourhis, K. Cosnuau, G. Guilmois, E. Rumilly, and E. Blangy, “ViEW: A wheelchair simulator for driving analysis,” Assistive Technology, 2020, https://doi.org/10.1080/10400435.2018.1503204.
- Y. Li, S. Dai, Y. Zheng, F. Tian, and X. Yan, “Modeling and kinematics simulation of a Mecanum wheel platform in RecurDyn,” Journal of Robotics, vol. 2018, no. 1, p. 9373580, 2018, https://doi.org/10.1155/2018/9373580.
- Z. Hendzel and Ł. Rykała, “Modelling of dynamics of a wheeled mobile robot with Mecanum wheels with the use of Lagrange equations of the second kind,” International Journal of Applied Mechanics and Engineering, vol. 22, no. 1, pp. 85–101, 2017, https://doi.org/10.1515/ijame-2017-0005.
- M. Hijikata, R. Miyagusuku, and K. Ozaki, “Wheel arrangement of four omni wheel mobile robot for compactness,” Applied Sciences, vol. 12, no. 12, p. 5798, 2022, https://doi.org/10.3390/app12125798.
- F. Isdaryani, F. Feriyonika, and R. Ferdiansyah, “Comparison of Ziegler-Nichols and Cohen Coon tuning method for magnetic levitation control system,” Journal of Physics: Conference Series, vol. 1450, no. 1, p. 012033, 2020, https://doi.org/10.1088/1742-6596/1450/1/012033.
- H. Torres-Salinas, J. Rodríguez-Reséndiz, E. E. Cruz-Miguel, and L. A. Ángeles-Hurtado, “Fuzzy logic and genetic-based algorithm for a servo control system,” Micromachines, vol. 13, no. 4, Art. no. 586, 2022, https://doi.org/10.3390/mi13040586.
- M. Luo, J. A. Duan, and Z. Yi, “Speed tracking performance for a coreless linear motor servo system based on a fitted adaptive fuzzy controller,” Energies, vol. 16, no. 3, Art. no. 1259, 2023, https://doi.org/10.3390/en16031259.
- E. H. Kadhim and A. T. Abdulsadda, “Mini drone linear and nonlinear controller system design and analyzing,” Journal of Robotics and Control (JRC), vol. 3, no. 2, pp. 212-218, 2022, https://doi.org/10.18196/jrc.v3i2.14180.
- W. Chen, S. K. Chen, Y. H. Liu, Y. J. Chen, and C. S. Chen, “An electric wheelchair manipulating system using SSVEP-based BCI system,” Biosensors, vol. 12, no. 10, Art. no. 772, 2022, https://doi.org/10.3390/bios12100772.
- D. Kumar, R. Malhotra, and S. R. Sharma, “Design and construction of a smart wheelchair,” Procedia Computer Science, vol. 172, pp. 302-307, 2020, https://doi.org/10.1016/j.procs.2020.05.048.
- M. R. Islam, M. R. T. Hossain, and S. C. Banik, “Synchronizing of stabilizing platform mounted on a two-wheeled robot,” Journal of Robotics and Control (JRC), vol. 2, no. 6, pp. 552-558, 2021, https://doi.org/10.18196/jrc.26136.
- A. O. Amole, O. E. Olabode, D. O. Akinyele, and S. G. Akinjobi, “Optimal Temperature Control Scheme for Milk Pasteurization Process Using Different Tuning Techniques for a Proportional Integral Derivative Controller,” Iranian Journal of Electrical and Electronic Engineering, vol. 2170, pp. 2170-2170, 2022, https://doi.org/10.22068/IJEEE.18.3.2170.
- P. Saini and C. Sharma, “Comparative Analysis of Controller Tuning Techniques for Dead Time Processes,” International Journal of Mathematical, Engineering and Management Sciences, vol. 4, no. 3, pp. 803, 2019, https://doi.org/10.33889/IJMEMS.2019.4.3-063.
- S. W. Shneen, H. S. Dakheel, and Z. B. Abdullah, “Design and implementation of no load, constant and variable load for DC servo motor,” Journal of Robotics and Control (JRC), vol. 4, no. 3, pp. 323–329, 2023, https://doi.org/10.18196/jrc.v4i3.17387.
- Z. Qu, H. Liu, Z. Wang, J. Xu, P. Zhang, and H. Zeng, “A combined genetic optimization with AdaBoost ensemble model for anomaly detection in buildings electricity consumption,” Energy and Buildings, vol. 248, Art. no. 111193, 2021, https://doi.org/10.1016/j.enbuild.2021.111193.
- A. Sharkawy and J. Nazzal, “Design and manufacturing using 3D printing technology of a 5-DOF manipulator for industrial tasks,” International Journal of Robotics and Control Systems, vol. 4, no. 2, pp. 893–909, 2024, https://doi.org/10.31763/ijrcs.v4i2.1456.
- A. W. Hidayat, I. Sulistiyowati, A. Wicaksono, and S. Syahrorini, “Hybrid system prototype for dam water level control system to irrigating rice fields,” Buletin Ilmiah Sarjana Teknik Elektro, vol. 6, no. 1, pp. 25–33, 2024, https://doi.org/10.12928/biste.v6i1.10016.
- K. Kunal, A. Z. Arfianto, J. E. Poetro, F. Waseel, and R. A. Atmoko, “Accelerometer implementation as feedback on 5 degree of freedom arm robot,” Journal of Robotics and Control (JRC), vol. 1, no. 1, pp. 31–34, 2020, https://doi.org/10.18196/jrc.1107.
- F. Ahmmed, A. Rahman, A. Islam, A. Alaly, S. Mehnaj, P. Saha, and T. Hossain, “Arduino-controlled multi-function robot with Bluetooth and nRF24L01+ communication,” International Journal of Robotics and Control Systems, vol. 4, no. 3, pp. 1353–1381, 2024, https://doi.org/10.31763/ijrcs.v4i3.1517.
- A. Prasetyo, J. Jamaaluddin, and I. Anshory, “PCB (Printed Circuit Board) etching machine using ESP32-Camera based Internet of Things,” Buletin Ilmiah Sarjana Teknik Elektro, vol. 5, no. 2, pp. 260–268, 2023, https://doi.org/10.12928/biste.v5i2.8132.
- Y. Irawan, M. Muhardi, R. Ordila, and R. Diandra, “Automatic floor cleaning robot using Arduino and ultrasonic sensor,” Journal of Robotics and Control (JRC), vol. 2, no. 4, pp. 240–243, 2021, https://doi.org/10.18196/jrc.2485.
- Y. Irawan, R. Wahyuni, and H. Fonda, “Folding clothes tool using Arduino Uno microcontroller and gear servo,” Journal of Robotics and Control (JRC), vol. 2, no. 3, pp. 170–174, 2021, https://doi.org/10.18196/jrc.2373.
- M. H. Zulwidad and I. Sulistiyowati, “Efficiency through automation: A single system for multiple railway guard posts,” Buletin Ilmiah Sarjana Teknik Elektro, vol. 5, no. 3, pp. 407–416, 2023, https://doi.org/10.12928/biste.v5i3.9001.
- T. Triwiyanto, W. Caesarendra, V. Abdullayev, A. A. Ahmed, and H. Herianto, “Single lead EMG signal to control an upper limb exoskeleton using embedded machine learning on Raspberry Pi,” Journal of Robotics and Control (JRC), vol. 4, no. 1, pp. 35–45, 2023, https://doi.org/10.18196/jrc.v4i1.17364.
- A. Juliano, A. H. Hendrawan, and R. Ritzkal, “Information system prototyping of strawberry maturity stages using Arduino Uno and TCS3200,” Journal of Robotics and Control (JRC), vol. 1, no. 3, pp. 86–91, 2020, https://doi.org/10.18196/jrc.1319.
- A. Muqaffi Siswanto and M. Muchlas, “Prototype of automatic sorting of goods in cosmetics warehouse,” Buletin Ilmiah Sarjana Teknik Elektro, vol. 4, no. 3, pp. 142–151, 2023, https://doi.org/10.12928/biste.v4i3.6919.
- K. Khairunisa, M. Mardeni, and Y. Irawan, “Smart aquarium design using Raspberry Pi and Android based,” Journal of Robotics and Control (JRC), vol. 2, no. 5, pp. 368–372, 2021, https://doi.org/10.18196/jrc.25109.
- A. A. Sahrab and H. M. Marhoon, “Design and fabrication of a low-cost system for smart home applications,” Journal of Robotics and Control (JRC), vol. 3, no. 4, pp. 409–414, 2022, https://doi.org/10.18196/jrc.v3i4.15413.
- F. N. Abdullah, G. A. Aziz, and S. W. Shneen, “Simulation model of servo motor by using MATLAB,” Journal of Robotics and Control (JRC), vol. 3, no. 2, pp. 176–179, 2022, https://doi.org/10.18196/jrc.v3i2.13959.
AUTHOR BIOGRAPHY

| Nuntachai Thongpance He currently holds the position of Associate Professor and Dean of the College of Biomedical Engineering at Rangsit University. He established undergraduate and graduate courses in medical instrumentation and biomedical engineering at Rangsit University. Nuntachai earned his Master of Engineering in nuclear technology from Chulalongkorn University in 1987 and his Bachelor of Science in physics with second-class honors from Prince of Songkla University in 1984. His research interests encompass medical devices, biomedical engineering, and healthcare management engineering. E-mail : nuntachai.t@rsu.ac.th |
|
|

| Phichitphon Chotikunnan He serves as a Lecturer in the Biomedical Engineering Program at the College of Biomedical Engineering, Rangsit University. Holding a Doctor of Engineering degree in Electrical and Information Engineering and a Master of Engineering in Electrical Engineering, both from King Mongkut's University of Technology Thonburi, he also earned a Bachelor of Engineering in Mechatronics Engineering from Pathumwan Institute of Technology, his research interests encompass robotics, embedded systems, fuzzy logic control, and iterative learning control. E-mail : phichitphon.c@rsu.ac.th (Corresponding Author) |
|
|

| Anantasak Wongkamhang He serves as a Lecturer in the Biomedical Engineering Program at the College of Biomedical Engineering, Rangsit University. He holds a Bachelor's degree in Medical Instrumentation from Rangsit University (2006) and a Master's degree in Biomedical Engineering from King Mongkut's Institute of Technology Ladkrabang (2014). His research interests span medical devices, equipment calibration, hospital engineering, microcontrollers, and instrumentation. E-mail : anantasak.w@rsu.ac.th |
|
|

| Rawiphon Chotikunnan He is a Lecturer in the Biomedical Engineering Program at the College of Biomedical Engineering, Rangsit University. With a Master of Engineering in Biomedical Engineering from Rangsit University and a Bachelor of Information Technology in Interactive Design and Game Development from Dhurakij Pundit University, his Research Interests Include Interactive Media, Medical Image Processing, Robots, and Control Systems. E-mail : rawiphon.c@rsu.ac.th |
|
|

| Pariwat Imura He serves as a Lecturer in the Biomedical Engineering Program at the College of Biomedical Engineering, Rangsit University. He holds a Master of Engineering in Biomedical Engineering from Rangsit University and completed his Bachelor of Science Program in Computer Science at Rajamangala University of Technology Lanna. His research interests span Medical Imaging Systems, Fundamental Principles of Computer Communication Networks and Database Management, Smart Medical Systems, Big Data Analytics in Medical, Medical Artificial Intelligence, and embedded systems. E-mail : pariwat.i@rsu.ac.th |
|
|

| Wanida Khotakham She obtained her Bachelor of Engineering in Automation Engineering from King Mongkut's University of Technology Thonburi, Thailand and her Master of Science in Data Science from Newcastle University, UK. Currently, she is a lecturer in the College of Biomedical Engineering at Rangsit University, where she teaches courses on software design, health information technology, data analytics, and automation engineering. E-mail : wanida.k@rsu.ac.th |
|
|

| Anuchit Nirapai He obtained his Bachelor of Science in Communication Engineering from Srinakharinwirot University, his Master of Science in Communication Engineering from King Mongkut's University of Technology North Bangkok, and his Doctor of Philosophy program in Information Technology Management from Mahidol University Thailand in 2008, 2015, and 2023, respectively. Presently, he holds a position as a lecturer in the College of Biomedical Engineering at Rangsit University. In this role, he instructs courses on software design, health information technology, information technology management, and the Internet of Medical Things (IoMT). E-mail : anuchit.ni@rsu.ac.th |
|
|

| Kittipan Roongprasert He is a Lecturer in the Biomedical Engineering Program at the College of Biomedical Engineering, Rangsit University, with a Bachelor’s degree in Medical Instrumentation from Rangsit University (2006) and a Master’s degree in Biomedical Engineering from King Mongkut's Institute of Technology Ladkrabang (2016). His research interests include medical devices, equipment calibration, microcontrollers, and instrumentation. E-mail: kittipan.r@rsu.ac.th |
|
|
Comparative Analysis of PID Tuning Methods for Speed Control in Mecanum-Wheel Electric Wheelchairs (Nuntachai Thongpance)