Buletin Ilmiah Sarjana Teknik Elektro ISSN: 2685-9572
HNIHA: Hybrid Nature-Inspired Imbalance Handling Algorithm to Addressing Imbalanced Datasets for Improved Classification: In Case of Anemia Identification
Dimas Chaerul Ekty Saputra 1, Tri Ratnaningsih 2, Irianna Futri 3, Elvaro Islami Muryadi 4,
Raksmey Phann 5, Su Sandi Hla Tun 6, Ritchie Natuan Caibigan 7
1 Department of Informatics, School of Computing, Telkom University Surabaya, Surabaya 60231, Indonesia
2 Department of Clinical Pathology and Laboratory Medicine, Faculty of Medicine, Public Health and Nursing, Universitas Gadjah Mada, Yogyakarta 55281, Indonesia
3 Department of International Technology and Innovation Management, International College, Khon Kaen University, Khon Kaen 40002, Thailand
4 Department of Public Health, Faculty of Health Sciences, Adiwangsa Jambi University, Jambi 36138, Indonesia
5 Department of Data Science, Seoul National University of Science and Technology, Seoul 01811, South Korea
6 Department of Human Movement Sciences, Faculty of Associated Medical Sciences, Khon Kaen University, Khon Kaen 40002, Thailand
7 Department of Computer Science and Information Technology, College of Informatics and Computing Sciences, Batangan State University – The National Engineering University, Batangas, 4217, Philippines
ARTICLE INFORMATION |
| ABSTRACT |
Article History: Received 07 August 2024 Revised 25 September 2024 Published 27 September 2024 |
| 
This study presents a comprehensive evaluation of three ensemble models designed to handle imbalanced datasets. Each model incorporates the hybrid nature-inspired imbalance handling algorithm (HNIHA) with matthews correlation coefficient and synthetic minority oversampling technique in conjunction with different base classifiers: support vector machine, random forest, and LightGBM. Our focus is to address the challenges posed by imbalanced datasets, emphasizing the balance between sensitivity and specificity. The HNIHA algorithm-guided support vector machine ensemble demonstrated superior performance, achieving an impressive matthews correlation coefficient of 0.8739, showcasing its robustness in balancing true positives and true negatives. The f1-score, precision, and recall metrics further validated its accuracy, precision, and sensitivity, attaining values of 0.9767, 0.9545, and 1.0, respectively. The ensemble demonstrated its ability to minimize prediction errors by minimizing the mean squared error and root mean squared error to 0.0384 and 0.1961, respectively. The HNIHA-guided random forest ensemble and HNIHA-guided LightGBM ensemble also exhibited strong performances. |
Keywords: Imbalanced Classification; Natured Inspired Algorithm; MCC; SMOTE; SVM |
Corresponding Author: Dimas Chaerul Ekty Saputra, School of Computing, Telkom University Surabaya, Surabaya 60231, Indonesia. Email: dimaschaerulekty@telkomuniversity.ac.id |
This work is licensed under a Creative Commons Attribution-Share Alike 4.0 
|
Document Citation: D. C. E. Saputra, T. Ratnaningsih, I. Futri, E. I. Muryadi, R. Phann, S. S. H. Tun, and R. N. Caibigan, “HNIHA: Hybrid Nature-Inspired Imbalance Handling Algorithm to Addressing Imbalanced Datasets for Improved Classification: In Case of Anemia Identification,” Buletin Ilmiah Sarjana Teknik Elektro, vol. 6, no. 3, pp. 254-270, 2024, DOI: 10.12928/biste.v6i3.11306. |
- INTRODUCTION
In the field of classification, constructing effective models depends on finding the right balance between available training data and the model's predictive ability [1]. Imbalanced datasets can significantly impact model performance in classification tasks, where the primary objective is to assign predefined labels to instances [2]-[6]. Imbalance, which is characterized by an uneven distribution of instances among classes, can introduce challenges that hinder the model's ability to generalize accurately [7][8]. Classifiers trained on imbalanced data may exhibit a bias towards the majority class, resulting in suboptimal accuracy and sensitivity, particularly for minority classes [9][10].
This paper addresses the challenge of imbalanced datasets by introducing the Hybrid nature-inspired imbalance handling algorithm (HNIHA). HNIHA integrates optimization techniques, leveraging the flower pollination algorithm (FPA), with strategic undersampling and oversampling strategies guided by the Matthews Correlation Coefficient (MCC) [11]. The use of the MCC is essential in optimizing fitness evaluations during the undersampling process [12]. This ensures that instances are strategically removed to enhance the model's generalization capabilities.
Optimizing models within imbalanced datasets presents a primary challenge due to the biased nature of the training process [13]. Traditional optimization algorithms may prioritize the majority class, as their objective functions do not account for the imbalance [14]. This results in classifiers that struggle to discern patterns within the minority class, leading to diminished sensitivity and overall model performance. In scenarios where the imbalance ratio fluctuates, a dynamic and adaptive optimization approach is necessary to achieve a balance between exploration and exploitation in the solution space [15]-[17].
Additionally, the optimization process encounters complexities when handling imbalanced datasets that undergo concept drift. Concept drift is the phenomenon where the statistical properties of the target variable change over time. This poses a challenge for traditional optimization algorithms that assume a static environment [18]-[20]. To address this challenge, the HNIHA incorporates dynamic adaptation mechanisms. HNIHA's adaptability is crucial in navigating the changing landscape of imbalanced datasets to ensure the optimization process remains effective.
The high dimensionality of feature spaces in many real-world datasets also presents computational challenges for optimization algorithms, in addition to biased training and concept drift. Traditional optimization techniques may face challenges in efficiently exploring and exploiting the solution space, resulting in increased computational costs and suboptimal convergence [21]-[24]. To mitigate these issues, FPA is strategically employed within HNIHA. FPA's adaptability and efficiency in handling high-dimensional spaces make it a suitable candidate for optimizing imbalanced datasets [25][26].
To emphasize the importance of balancing datasets, it is crucial to consider the impact of imbalanced data on classification outcomes [27][28]. Imbalance can cause classifiers to be biased towards the majority class, resulting in models that struggle to accurately predict minority class instances [4]. This bias induced by imbalance can be harmful in scenarios where minority class instances carry critical information, such as in the medical diagnoses [29][30]. Achieving a balanced dataset is crucial for models that aim to provide fair, accurate, and inclusive predictions across all class [31].
Empirical evidence from classification processes demonstrates the necessity of balanced datasets. A classifier trained on imbalanced data may appear to have high accuracy, but this metric can be misleading [5],[32]. The accuracy of the model may be largely attributed to the majority class, while its ability to correctly predict instances from the minority class remains compromised. This phenomenon is particularly problematic when the minority class holds significant importance, and misclassifying instances from this class can have severe consequences [5],[33][34].
The use of the MCC in HNIHA reinforces the importance of balanced datasets. MCC considers true positives, true negatives, false positives, and false negatives, providing a more comprehensive evaluation metric that balances sensitivity and specificity [35]. HNIHA incorporates MCC into the fitness evaluation when undersampling to guide the removal of instances and enhance the model's predictive capabilities across all classes. The synthetic minority over-sampling technique (SMOTE) is a pivotal component of HNIHA's oversampling strategy [33],[36]. Imbalanced datasets frequently lack sufficient instances of the minority class for the model to learn its patterns effectively [37][38]. SMOTE addresses the challenge of class imbalance by generating synthetic instances for the minority class. This augments the dataset and provides the model with more diverse examples to learn from [39]-[42].
The integration of SMOTE ensures that HNIHA not only rectifies the imbalance but also empowers the model to make more accurate predictions for minority class instances. HNIHA provides a comprehensive solution to the challenges posed by imbalanced datasets in classification tasks. HNIHA incorporates the FPA, MCC, and SMOTE, making it a novel approach in the evolving landscape of imbalanced learning. HNIHA aims to redefine classification paradigms by offering accurate, inclusive, and fair models for all classes. The company achieves this through dynamic adaptability and optimization prowess while committing to a balanced dataset.
One important aspect concerns the diagnosis of anemia in the human body [43]. Although blood tests are crucial for detecting anemia, they can be quite expensive. Therefore, there is a need for more cost-effective alternative haematological tests to predict the level of anemia, especially for individuals with anemia, those showing indications of anemia, and individuals dealing with cancer. Several tests can be used to measure different aspects of blood, including haemoglobin (Hb), haematocrit (HCT), red blood cells (RBC), mean corpuscular volume (MCV), mean corpuscular haemoglobin (MCH), mean corpuscular haemoglobin concentration (MCHC), and red blood cell distribution width (RDW).
Building upon these facts, the objective of this research is to employ the HNIHA model for addressing classification challenges associated with imbalanced datasets. This study makes significant contributions in three key aspects, namely:
- The HNIHA model was used to create a new classification model by combining machine learning and nature-inspired algorithms, resulting in a set of HNIHAs.
- The factors considered important in the classification process were retained, even if they had a minor impact on the dataset.
- Offering an alternative classification model that includes multiple independent variables while maintaining a manageable dataset size and accounting for imbalanced data characteristics.
This paper is divided into five sections. Part 1 serves as an introduction, providing an overview of the problem's background, outlining objectives, and detailing research contributions. Section 2 covers related works derived from an extensive literature review. Section 3 is dedicated to the materials and methods employed in the study. Section 4 explains the research results, and discusses also supports the findings through a comparative analysis with other studies. Finally, Section 5 summarizes the conclusions and provides recommendations for future research.
- RELATED WORKS
- Flower Pollination Algorithm
The Flower Pollination Algorithm (FPA) is a metaheuristic optimization algorithm inspired by the pollination process of flowering plants. It was introduced by Xin-She Yang in 2012 and is designed for numerical optimization problems [44]. FPA initializes potential solutions, referred to as 'flowers,' randomly. The algorithm evaluates the fitness of each solution based on the given objective function. The essence of FPA is in simulating pollination, where flowers with higher fitness share information with less fit neighbours. FPA involves several mathematical formulas to represent its key steps, such as initialization, objective function, local pollination, and global pollination [45][46]. For initialization denoted as
| 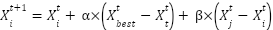
| (1) |
where 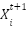 update the position of the current flower,
update the position of the current flower, 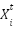 is the position of
is the position of 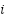 -th flower in the population at iteration
-th flower in the population at iteration 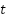 .
. 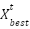 is the position of the global best flower in the population at iteration
is the position of the global best flower in the population at iteration 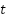 .
. 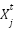 is the position of a randomly selected flower (neighbor) in the population at iteration
is the position of a randomly selected flower (neighbor) in the population at iteration 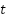 .
. 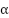 and
and 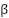 are scaling factors that control the influence of global and local pollination, respectively.
are scaling factors that control the influence of global and local pollination, respectively.
The exchange of information occurs through both local and global pollination processes, facilitating the dissemination of valuable knowledge throughout the population [47]. Local pollination updates less fit solutions using information from their fitter neighbours, while global pollination enables the entire population to be influenced by the best solutions found thus far [48]. The iterative process of pollination and updating continues until a termination criterion is met [49]. The FPA aims to strike a balance between exploration and exploitation, making it suitable for solving a variety of optimization problems in engineering [50], science [51], and other domains [52].
- Synthetic Minority Over-sampling Technique
SMOTE is a method utilized in machine learning and data mining to tackle the class imbalance problem [53]. This problem arises when the number of instances of one class, usually the minority class, is significantly lower than the number of instances of the other class, the majority class [54]. This imbalance can result in biased models that perform poorly on the minority class [55]. The main formula of SMOTE denoted as
| 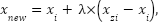
| (2) |
where 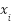 is an instance from the minority class,
is an instance from the minority class, 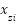 is one of the k-nearest neighbor of
is one of the k-nearest neighbor of 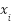 ,
, 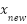 is the synthetic instance generated between
is the synthetic instance generated between 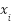 and
and 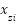 , and
, and  is a random number between 0 and 1.
is a random number between 0 and 1.
This formula essentially performs a linear interpolation between the minority instance 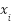 and one of its k-nearest neighbors
and one of its k-nearest neighbors 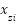 . The random parameter
. The random parameter  controls the position of the synthetic instance along the line connecting
controls the position of the synthetic instance along the line connecting 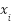 and
and 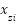 . By varying
. By varying  , multiple synthetic instances can be generated. The process is repeated for each instance in the minority class, creating a set of synthetic instances that can be added to the original dataset to balance the class distribution. The goal is to provide the machine learning algorithm with a more balanced training set, which can improve the performance of the model, especially in cases where the class distribution is severely skewed.
, multiple synthetic instances can be generated. The process is repeated for each instance in the minority class, creating a set of synthetic instances that can be added to the original dataset to balance the class distribution. The goal is to provide the machine learning algorithm with a more balanced training set, which can improve the performance of the model, especially in cases where the class distribution is severely skewed.
- Matthews Correlation Coefficient
The Matthews Correlation Coefficient (MCC) is a metric used in binary classification to evaluate how a classifier performs [56]. It provides a balanced measure of a model's performance, taking into account true positives 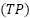 , true negatives
, true negatives 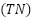 , false positives
, false positives 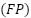 , and false negatives
, and false negatives 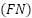 .
.
| 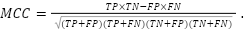
| (3) |
TP represents the number of true positives, which are instances that were correctly predicted as positive. TN represents the number of true negatives, which are instances that were correctly predicted as negative. FP represents the number of false positives, which are instances that were predicted as positive but are negative. FN represents the number of false negatives, which are instances that were predicted as negative but are positive.
This formula provides a single metric that evaluates the performance of binary classification models by combining positive and negative predictions. The resulting MCC value ranges from 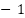 to
to 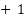 , where
, where 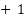 indicates perfect prediction, 0 indicates random prediction, and
indicates perfect prediction, 0 indicates random prediction, and 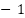 indicates total disagreement between prediction and observation [12],[57].
indicates total disagreement between prediction and observation [12],[57].
- MATERIALS AND METHODS
This section will elucidate the dataset utilized, detail the proposed model, and delineate the model testing process. To establish the reliability of the proposed model, a comparative analysis will be conducted employing support vector machine (SVM), random forest (RF), and light gradient boosting machine (LightGBM) methods. This rigorous comparison aims to validate the effectiveness and robustness of the proposed model against established machine learning algorithms.
3.1. Materials
The study included 128 patients, all diagnosed with various forms of anemia. The data used in this research came from the Clinical Pathology Laboratory of RSUP Dr. Sardjito Yogyakarta, Indonesia, and the Department of Clinical Pathology and Laboratory Medicine, Faculty of Medicine, Public Health and Nursing, Gadjah Mada University. Hematological measurements were obtained from patients diagnosed with beta-thalassemia trait (BTT) and iron deficiency anemia (IDA). It is important to note that the Medical and Health Research Ethics Committee (MHREC) of the Faculty of Medicine, Public Health, and Nursing at Dr. Sardjito, Gadjah Mada University, Yogyakarta, Indonesia issued an ethics approval letter marked KE/FK/1255/EC/2021 for the implementation of this research, ensuring adherence to ethical standards. The analysis considered several parameters, including RBC, Hb, HCT, MCV, MCH, MCHC, and RDW. Table 1 provides definitions for some of the acronyms used in the investigation.
Table 1. Abbreviation and Data Profile
Parameter | Abbreviation | Unit | Data Profile |
Standard Deviation | Minimum | Maximum | Average |
Red Blood Cell | RBC | 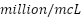
| 3.77 | 29.4 | 48.5 | 37.18 |
Haemoglobin | Hb | 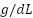
| 1.38 | 9.0 | 16.8 | 11.21 |
Haematocrit | HCT | 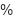
| 2.31 | 16.7 | 27.9 | 22.16 |
Mean Corpuscular Volume | MCV | 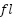
| 1.86 | 19.3 | 35.2 | 29.96 |
Mean Corpuscular Haemoglobin | MCH | 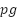
| 6.09 | 55.9 | 86.0 | 73.53 |
Mean Corpuscular Haemoglobin Concentration | MCHC | 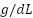
| 0.57 | 3.78 | 6.94 | 5.08 |
Red-cell Distribution Width | RDW | 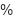
| 1.44 | 13.6 | 21.2 | 16.97 |
Our exclusion criteria were as follows: 1) the patients has MCV 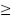 80 fL and MCH
80 fL and MCH 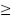 27 pg; 2) the patients has Hb
27 pg; 2) the patients has Hb 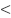 9 g/dL. Before processing the data, we apply StandardScaler. In machine learning, StandardScaler is typically applied to each feature independently and rescales it so that the mean (average) of the feature is 0 and the standard deviation is 1 [58]. This transformation is crucial in scenarios where features in the dataset have different scales, which can prevent some machine learning algorithms from performing well. The formula for StandardScaler denoted as. Where
9 g/dL. Before processing the data, we apply StandardScaler. In machine learning, StandardScaler is typically applied to each feature independently and rescales it so that the mean (average) of the feature is 0 and the standard deviation is 1 [58]. This transformation is crucial in scenarios where features in the dataset have different scales, which can prevent some machine learning algorithms from performing well. The formula for StandardScaler denoted as. Where 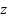 is the standardized value,
is the standardized value, 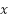 is the original value,
is the original value, 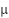 is the mean of the feature, and
is the mean of the feature, and 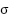 is the standard deviation of the feature. Python is used for data processing.
is the standard deviation of the feature. Python is used for data processing.
| 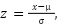
| (4) |
3.2. Proposed Model: HNIHA
The proposed model uses a combination of FPA, MCC, and SMOTE to optimize the balance of data within the training set. For classification, the model employs SVM due to its resilience against overfitting, which is a common concern in scenarios with limited datasets. The primary objective of maximizing margins in SVMs significantly contributes to effective generalization, which is a critical attribute when dealing with a limited pool of training examples. SVMs are particularly advantageous in such situations because they meticulously create a clear and wide margin between different classes, which fortifies the stability of the decision boundary.
Support vectors that encapsulate the most informative aspects of the data are emphasized by SVM to mitigate the risk of capturing noise or outliers during training. This approach not only refines the model's adaptation to new, unseen instances but also enhances its overall reliability in the face of a scarcity of training examples. The emphasis on creating a robust and well-defined margin further contributes to the model's adeptness in generalizing effectively. The adaptability of SVMs is enhanced by the incorporation of kernel functions, which allows for the capture of complex relationships within the data. This feature is especially useful when dealing with limited datasets that may exhibit intricate patterns.
The HNIHA is a combination of the FPA, MCC loss function, and SMOTE. It is designed to address imbalanced datasets by utilizing the MCC loss as a fitness measure. The MCC loss incorporates TP, TN, FP, and FN to evaluate the performance of the classifier. The FPA facilitates the optimization process by updating the positions of flowers through Levy flights and random selections [59]. This approach converges towards a solution that minimizes the MCC loss.
To evaluate the fitness of each flower, a classifier is trained on synthetic instances generated using the FPA solution. The FPA solution is applied to the original samples to produce synthetic instances, resulting in a balanced dataset. This process ensures that the algorithm learns from the synthesized data, improving its ability to handle imbalances. The SMOTE algorithm enhances oversampling by generating synthetic instances within the minority class, thereby improving the classifier's discriminatory capabilities.
The process of synthetic instance generation involves calculating the difference between each original sample and the FPA solution. This difference is then added to the original sample, resulting in a synthetic instance that is clipped to ensure feature values fall within the valid range of [0, 1]. The algorithm iteratively applies this process to each sample in the dataset, adapting its synthetic instance generation strategy to the evolving FPA solution.
The MCC loss is calculated by negating the MCC. The MCC measures the correlation between predicted and true binary classifications, providing a balanced assessment, particularly for imbalanced datasets. The MCC loss aims to minimize misclassifications while considering both sensitivity and specificity denoted as
| 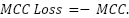
| (5) |
The fitness of each flower is determined by evaluating the MCC loss. The optimization of MCC loss is guided by the solution of the FPA. To generate synthetic instances for a given flower, we use SMOTE. A classifier is trained on the augmented data set, and the MCC loss is calculated based on the predictions made on the original data set denoted as
| 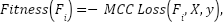
| (6) |
where,
| 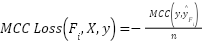 , ,
| (7) |
where 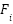 represents the
represents the 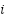 -th flower,
-th flower, 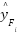 is the prediction of the classifier trained on the synthetic instances generated using
is the prediction of the classifier trained on the synthetic instances generated using 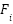 and
and 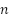 is the number of the flowers.
is the number of the flowers.
Algorithm 1 HNIHA |
Given: 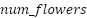 : Number of flowers (potential solutions) : Number of flowers (potential solutions)
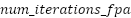 : Number of iterations for Flower Pollination Algorithm (FPA) : Number of iterations for Flower Pollination Algorithm (FPA)
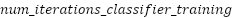 : Number of iterations for classifier training : Number of iterations for classifier training
Input: 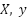 : Input imbalanced dataset : Input imbalanced dataset
Process: Perform Matthews Correlation Coefficient (MCC) Loss: Function MCC_Loss(y_true, y_pred): MCC = Calculate the MCC based on Equation (3) MCC_Loss = -MCC
Return MCC_Loss
Perform Flower Pollination Algorithm (FPA): flowers = Randomly_Initialize_Flowers(num_flowers) best_solution = None best_fitness = Infinity
For iteration in range(num_iterations_fpa): fitness_values = Evaluate_Fitness
For each flower in flowers: j, k = Randomly_Select_Two_Flowers based on Equation (1)
current_best_fitness = Minimum(fitness_values)
If current_best_fitness < best_fitness: best_fitness = current_best_fitness best_solution = flowers[IndexOf_Minimum(fitness_values)]
Perform Synthetic Instance Generation: X_train_augmented = Generate_Synthetic_Instances based on Equation (2)
Train Classifier on Augmented Dataset: classifier = Train_Classifier(X_train_augmented, y_train, num_iterations_classifier_training)
Evaluate Classifier Performance: mcc_test = Evaluate_Classifier(classifier, X_test, y_test)
Output: mcc_test |
Synthetic instances are created using the FPA solution. The difference between each original instance and the FPA solution is calculated. A synthetic instance is created by applying this difference to the original instance. Randomness guided by the Levy distribution is introduced by the Levy flight denoted as
| 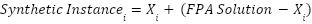
| (8) |
where 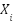 represents the
represents the 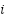 -th sample, and the FPA solution guides the generation of synthetic instances.
-th sample, and the FPA solution guides the generation of synthetic instances.
The dataset was optimized using HNIHA, and then SVM was used for classification. In the case of a linearly separable dataset, the hyperplane equation can be expressed as follows:
| 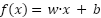 , ,
| (9) |
where, 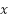 represents the input vector,
represents the input vector, 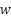 is the weight vector, and
is the weight vector, and 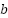 is the bias term.
is the bias term.
The decision function classifies a point based on the sign of 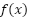 . If
. If 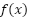 is positive, the point belongs to one class; if it's negative, the point belongs to the other class.
is positive, the point belongs to one class; if it's negative, the point belongs to the other class.
The margin is the distance between the hyperplane and the nearest data point of one of the two classes. For a point 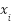 , the margin is given by:
, the margin is given by:
| 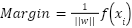
| (10) |
The objective is to optimize the margin while accurately classifying the training data. This results in the subsequent optimization problem:
| 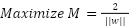
| (11) |
Subject to the constraints:
where, 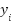 represents the class label of the ith data point, and
represents the class label of the ith data point, and 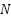 is the total number of data points.
is the total number of data points.
To solve the constrained optimization problem, Lagrange multipliers (a) are introduced for each constraint. The Lagrangian is then calculated by
| 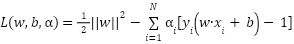
| (12) |
The problem can be transformed into its dual form by taking derivatives and setting them to zero. The optimal values for 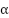 can be obtained by solving the dual problem.
can be obtained by solving the dual problem.
| 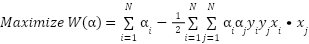
| (13) |
Subject to the constraints:
The non-zero 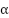 values correspond to the support vectors. These support vectors are the data points that determine the position of the hyperplane. The
values correspond to the support vectors. These support vectors are the data points that determine the position of the hyperplane. The 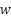 vector can be represented as a linear combination of the support vectors denoted as
vector can be represented as a linear combination of the support vectors denoted as
| 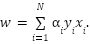
| (14) |
The bias term 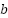 can be computed using any support vector:
can be computed using any support vector:
| 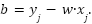
| (15) |
The HNIHA algorithm integrates the FPA, MCC loss function, and SMOTE to address imbalanced datasets. The FPA guides the optimization of the MCC loss. The synthetic instance generation, which incorporates SMOTE, helps to create a balanced training dataset. This holistic approach aims to enhance the classifier's ability to generalize and make accurate predictions on imbalanced data.
3.2. Model Testing
Model performance was evaluated using several metrics, including MCC, F1-Score, Precision, and Recall. Mean square error (MSE) and root mean square error (RMSE) were also used as a reliable measure of algorithm performance. The formula for MSE denoted as
| 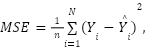
| (16) |
Root mean square error (RMSE) is a widely used metric for evaluating the accuracy of predictive models [60]. It is especially prevalent in the fields of statistics and machine learning for assessing the performance of regression models. RMSE measures the average magnitude of errors between predicted and observed values [61]. The formula for RMSE denoted as
| 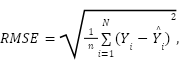
| (17) |
where 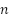 is the number of data points,
is the number of data points, 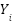 represents the observed values, and
represents the observed values, and 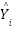 represents the predicted values.
represents the predicted values.
Subsequently, the obtained results will be compared to those derived from alternative methodologies, specifically the RF and LightGBM algorithms, to ensure objectivity in the testing process. To validate the model, it will be applied to data points in the training data. For model testing purposes, the algorithm is executed on data points that were excluded from the training process, also known as test data.
- RESULT AND DISCUSSION
Before delving deeper, we calculate the correlation coefficient for each variable concerning the target class. The outcomes are displayed in Table 2, revealing that MCV exhibits the highest correlation coefficient. This underscores the closest relationship between MCV and the occurrence of anemia.
Table 2. Correlation coefficient
Variable | Correlation coefficient |
RBC | -0.585073 |
Hb | -0.358959 |
HCT | -0.353653 |
MCV | 0.318985 |
MCH | 0.177136 |
MCHC | -0.165253 |
RDW | 0.232664 |
The dataset of 128 instances was partitioned into two sets: a training dataset and a testing dataset. The main objective of this research is to present an innovative model as an alternative solution to the challenges faced by SVM when dealing with datasets of moderate size. SVM is inherently resistant to overfitting, which is a common issue in scenarios with limited and imbalanced datasets. This research aims to evaluate the model's applicability across diverse datasets with HNIHA-SVM. The training and testing data are divided into 80% and 20%, respectively. Our dataset includes seven variables. To demonstrate the reliability of the method, we calculated the MSE for both HNIHA-RF and HNIHA-LightGBM.
After applying the model to the anemia dataset, the results, depicted in Figure 1, show a striking similarity between the anemia levels in the actual data and the HNIHA-SVM output. This resulted in a very low MSE of 0.0385, proving the efficacy of the proposed model in accurately reflecting anemia rates.
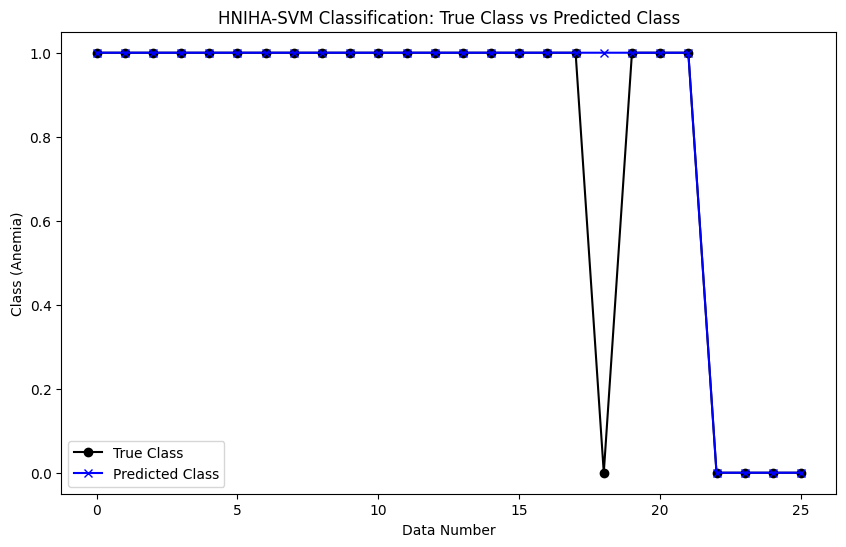
Figure 1. HNIHA-SVM Classification: True Class vs Predicted Class
However, the comparison becomes interesting when considering HNIHA-RF. Figure 2 shows a slight difference between the anemia levels in the real data and the HNIHA-RF output, resulting in a slightly higher MSE of 0.0769. These small differences encourage a closer examination of HNIHA-RF performance, revealing insights into its behavior in contrast to HNIHA-SVM models.
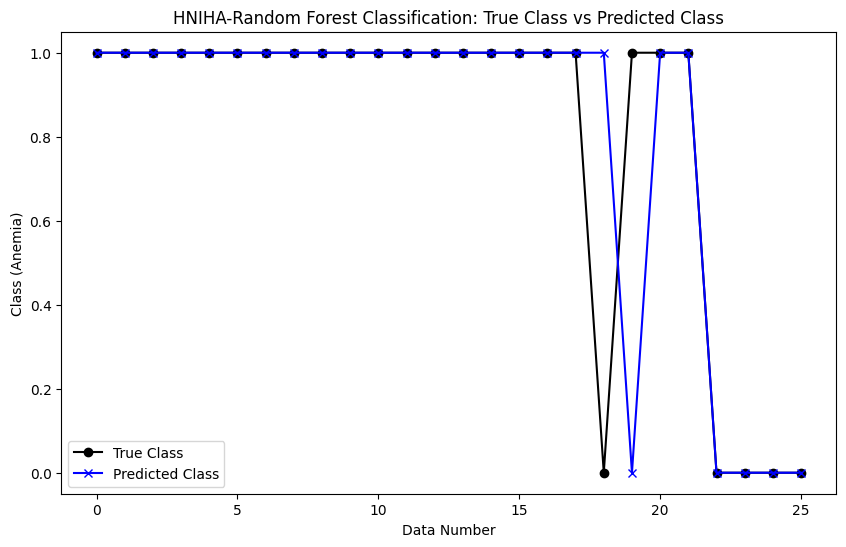
Figure 2. HNIHA-RF Classification: True Class vs Predicted Class
Additionally, Figure 3 illustrates a clearer difference between the anemia levels in the actual data and HNIHA-LightGBM output. The MSE in this case is 0.1154, indicating a significant deviation between predictions and real-world observations. These differences highlight the importance of methodological choice and algorithm selection in achieving accurate and reliable predictions, particularly in the context of anemia prediction in our dataset.
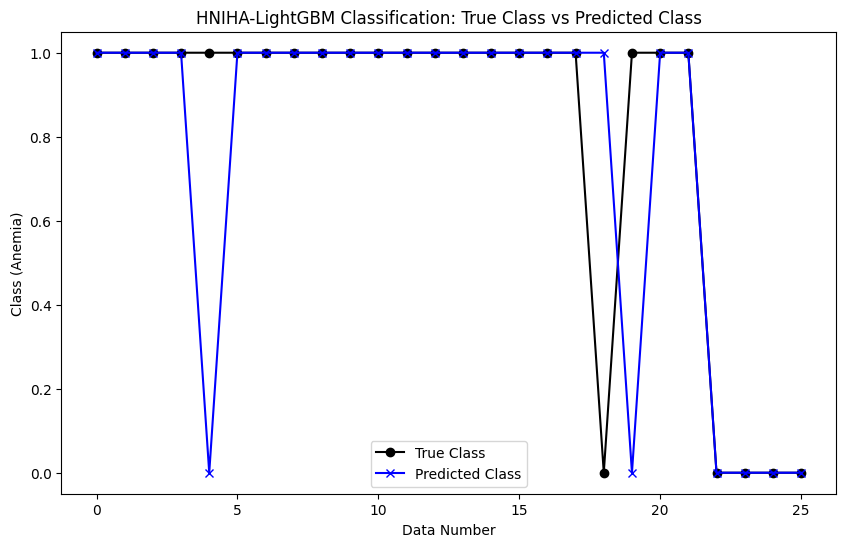
Figure 3. HNIHA-LightGBM Classification: True Class vs Predicted Class
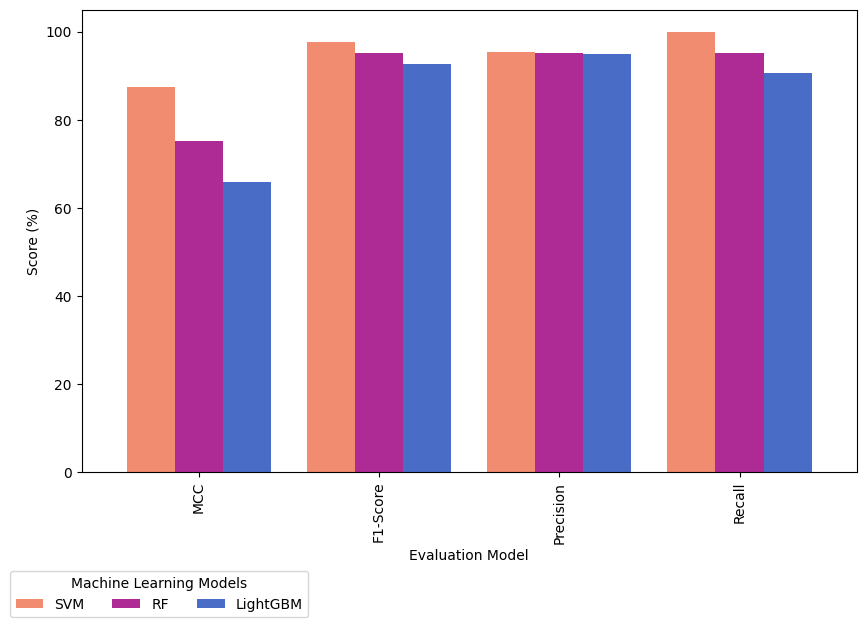
Figure 4 presents the performance metrics of three machine learning models: SVM, RF, and LightGBM. The metrics provide insights into the models' classification accuracy. The SVM model shows exceptional performance with a Matthews Correlation Coefficient (MCC) of 87.39, indicating a strong correlation between its predictions and actual outcomes. The model achieves a high F1-Score of 97.67, indicating a balanced trade-off between precision and recall. The SVM model has a Precision of 95.45 and a Recall of 100, correctly identifying positive instances while minimizing false positives. The Random Forest (RF) model also demonstrates commendable performance, although slightly trailing behind SVM. The MCC of 75.24 suggests a strong correlation between predictions and actual outcomes. The model achieves a balanced F1-Score, Precision, and Recall of 95.24, indicating robust classification across different classes. In comparison, LightGBM exhibits a lower MCC of 65.92, indicating a weaker correlation between its predictions and actual outcomes. Despite this, the model achieves a reasonable F1-Score of 92.68, with a Precision of 95.00 and a Recall of 90.48. In summary, the models can be ranked based on MCC, with SVM leading, followed by RF, and then LightGBM. However, selecting the most appropriate model depends on the specific requirements and trade-offs inherent in the application.

Figure 4. Evaluation Model Comparison
The receiver operating characteristic (ROC) is a widely used graphical representation and evaluation metric in binary classification tasks [62]. It shows the trade-off between the True positive rate (sensitivity) and the false positive rate (1 - specificity) across varying classification thresholds. Figure 5, an ROC score from HNIHA-SVM is 0.90 indicating a highly effective model, reflecting a strong ability to discriminate between the positive and negative classes. A score of 0.90 indicates that the model has a high true positive rate and a relatively low false positive rate. This highlights its ability to correctly identify positive instances while minimizing the risk of misclassifying negative instances. A ROC score of 0.90 is indicative of a well-calibrated and accurate classifier, making it a valuable metric for assessing the overall performance of binary classification models.
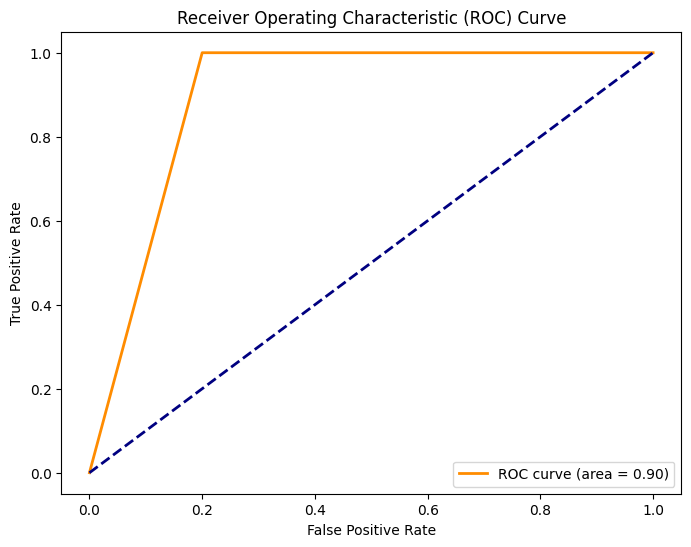
Figure 5. ROC HNIHA-SVM
SVM have remarkable advantages that make them stand out in the machine learning field [63]. One key strength is their proficiency in navigating high-dimensional spaces, making them particularly adept at tasks where the number of features exceeds the number of examples [64]. SVM strikes a balance between overfitting and robust performance with diverse datasets. They are also adaptable to smaller datasets without compromising accuracy. Additionally, SVM are versatile in decision-making. SVM can handle both linear and non-linear patterns in data through the use of different kernel functions, providing a flexible approach to capturing complex relationships. They offer a powerful toolset for crafting accurate and adaptable models across a range of machine learning applications, whether dealing with straightforward linear separations or more intricate, non-linear distinctions [65]-[68].
The HNIHA algorithm, which combines the Hybrid Nature-Inspired Imbalance Handling Algorithm with MCC Loss, along with SMOTE and SVM, forms a robust ensemble approach for handling imbalanced datasets. SMOTE plays a pivotal role in this ensemble by generating synthetic instances within the minority class to address the class imbalance. This augmentation leads to a more balanced and representative training dataset, which provides a solid foundation for improved generalization. Additionally, the HNIHA component optimizes the SVM classifier using the Flower Pollination Algorithm guided by the MCC loss and SMOTE. This dynamic optimization process ensures that the SVM adapts effectively to varying data distributions within the imbalanced dataset, contributing to enhanced generalization.
The adaptability of the ensemble to data dynamics is highlighted by the dynamic nature of both SMOTE and HNIHA. SMOTE adjusts its synthetic instance generation based on the local structure of the minority class, while HNIHA-MCC dynamically optimizes the FPA solution to evolving imbalanced scenarios. SVM's flexibility in selecting different kernel functions enables it to adapt to various data structures, adding another layer of adaptability to the ensemble. The ensemble approach enhances discriminatory power through the diversity introduced by SMOTE, preventing biases and aiding SVM in distinguishing between minority and majority classes. HNIHA optimization of MCC loss ensures a balanced trade-off between sensitivity and specificity, contributing to SVM's discriminatory capabilities. Fine-tuning SVM hyperparameters, such as the choice of kernel and regularization parameters, further refines its ability to discriminate between classes.
The synergy among these components creates a powerful ensemble that integrates nature-inspired optimization, data-level synthesis, and robust classification techniques. The combination of SMOTE, HNIHA-MCC, and SVM provides a comprehensive solution for imbalanced datasets, utilizing the unique strengths of each component. The ensemble is evaluated using a comprehensive set of metrics, including MCC loss, accuracy, precision, recall, and F1 Score, providing a thorough assessment of its effectiveness. This approach integrates a sophisticated strategy for handling imbalanced classification tasks, promising robust performance across diverse datasets and imbalanced scenarios.
The presented ensemble approach offers a balanced and synergistic solution compared to traditional methods that rely solely on resampling techniques or algorithmic adjustments. To overcome class imbalance, SMOTE generates synthetic instances, while the FPA optimizes the model dynamically, guided by MCC loss and adapting to the intricacies of imbalanced data. The proposed ensemble incorporates SVM to enhance robustness and discriminative power. SVMs are known for their ability to handle complex decision boundaries and diverse datasets. Unlike other popular ensemble techniques such as Random Forest or AdaBoost, which focus on combining weak learners, this ensemble uniquely integrates nature-inspired optimization and data-level synthesis with the strengths of SVMs. Although Random Forest and AdaBoost can be effective in some situations, their performance may vary when dealing with highly imbalanced datasets, and they may not explicitly optimize for metrics such as MCC, which balance sensitivity and specificity.
The ensemble approach shows promise in real-world scenarios where imbalanced datasets are prevalent [69]-[71]. For example, in healthcare, where minority class instances, such as rare diseases, are often underrepresented, the ensemble can aid in building robust predictive models [72][73]. Similarly, in financial fraud detection, where fraudulent activity is rare, the ensemble's ability to handle class unbalance ensures accurate identification of anomalies [74][75]. The adaptability of the ensemble to the changing dynamics of the data makes it suitable for domains with characteristics that evolve. This could include scenarios such as network intrusion detection or cybersecurity, where attack patterns may change, and the model needs to continuously adapt to emerging threats [76][77].
Although the ensemble approach provides a comprehensive solution, it is essential to consider computational resources and scalability, particularly in large-scale applications. Fine-tuning hyperparameters for both the FPA and SVM is a crucial step for achieving optimal performance. Furthermore, it is important to consider the interpretability of the ensemble, as the combination of different components may make it difficult to interpret feature importance or decision-making processes. In conclusion, the proposed ensemble approach, which integrates HNIHA, MCC, SMOTE, and SVM, presents a robust solution for handling imbalanced datasets. This unique combination of nature-inspired optimization, data-level synthesis, and robust classification offers a promising avenue for improving model performance in imbalanced scenarios. However, it is important to carefully consider specific application requirements and computational considerations during implementation.
- CONCLUSIONS
The integrated Hybrid Nature-Inspired Imbalance Handling Algorithm (HNIHA) with MCC Loss, Synthetic Minority Over-sampling Technique (SMOTE), and Support Vector Machines (SVM) ensemble proved to be a highly successful approach for addressing the challenges posed by imbalanced datasets. The performance of the ensemble was evaluated using a comprehensive set of metrics, demonstrating its effectiveness in handling both sensitivity and specificity in classification tasks. The Matthews Correlation Coefficient (MCC), a key guiding metric for the optimization process, yielded an impressive value of 0.8739. This indicates a well-balanced performance, considering both true positives and true negatives, highlighting the ensemble's ability to navigate the complexities of imbalanced data. The ensemble's success in achieving high predictive accuracy, precision, and sensitivity is further affirmed by the F1 Score, Precision, and Recall metrics. The F1 Score reached 0.9767, Precision was at 0.9545, and Recall was a perfect 1.0.
The Area Under the Curve (AUC) and Area Under the Precision-Recall curve (AUC-PR) scores, with values of 0.9 and 0.9773 respectively, reinforce the ensemble's capability to discriminate between classes and make well-calibrated predictions. The Mean Squared Error (MSE) and Root Mean Squared Error (RMSE) scores indicate minimal prediction errors, underscoring the ensemble's accuracy in capturing the underlying patterns within the imbalanced dataset. In conclusion, the proposed ensemble approach emerges as a powerful solution, seamlessly integrating nature-inspired optimization, data-level synthesis, and robust classification. The results demonstrate the efficacy of the solution in handling imbalanced datasets, with potential applications across various domains where accurate predictions on minority class instances are crucial. This ensemble is an adaptable and holistic solution that holds promise for advancing the state-of-the-art in imbalanced classification tasks.
REFERENCES
- J. Tanha, Y. Abdi, N. Samadi, N. Razzaghi, and M. Asadpour, “Boosting methods for multi-class imbalanced data classification: an experimental review,” J Big Data, vol. 7, no. 1, p. 70, 2020, https://doi.org/10.1186/s40537-020-00349-y.
- M. Koziarski, “Radial-Based Undersampling for imbalanced data classification,” Pattern Recognition, vol. 102, p. 107262, 2020, https://doi.org/10.1016/j.patcog.2020.107262.
- H. Liu, M. Zhou, and Q. Liu, “An embedded feature selection method for imbalanced data classification,” IEEE/CAA J. Autom. Sinica, vol. 6, no. 3, pp. 703–715, 2019, https://doi.org/10.1109/JAS.2019.1911447.
- F. Thabtah, S. Hammoud, F. Kamalov, and A. Gonsalves, “Data imbalance in classification: Experimental evaluation,” Information Sciences, vol. 513, pp. 429–441, 2020, https://doi.org/10.1016/j.ins.2019.11.004.
- P. Vuttipittayamongkol, E. Elyan, and A. Petrovski, “On the class overlap problem in imbalanced data classification,” Knowledge-Based Systems, vol. 212, p. 106631, 2021, https://doi.org/10.1016/j.knosys.2020.106631.
- N. W. S. Wardhani, M. Y. Rochayani, A. Iriany, A. D. Sulistyono, and P. Lestantyo, “Cross-validation Metrics for Evaluating Classification Performance on Imbalanced Data,” in 2019 International Conference on Computer, Control, Informatics and its Applications (IC3INA), pp. 14–18, 2019, https://doi.org/10.1109/IC3INA48034.2019.8949568.
- A. Ali-Gombe and E. Elyan, “MFC-GAN: Class-imbalanced dataset classification using Multiple Fake Class Generative Adversarial Network,” Neurocomputing, vol. 361, pp. 212–221, 2019, https://doi.org/10.1016/j.neucom.2019.06.043.
- Q. Wang, W. Cao, J. Guo, J. Ren, Y. Cheng, and D. N. Davis, “DMP_MI: An Effective Diabetes Mellitus Classification Algorithm on Imbalanced Data With Missing Values,” IEEE Access, vol. 7, pp. 102232–102238, 2019, https://doi.org/10.1109/ACCESS.2019.2929866.
- G. Douzas, F. Bacao, J. Fonseca, and M. Khudinyan, “Imbalanced Learning in Land Cover Classification: Improving Minority Classes’ Prediction Accuracy Using the Geometric SMOTE Algorithm,” Remote Sensing, vol. 11, no. 24, p. 3040, 2019, https://doi.org/10.3390/rs11243040.
- H. B. Jethva and P. A. Barot, “ImbTree: Minority Class Sensitive Weighted Decision Tree for Classification of Unbalanced Data,” ijisae, vol. 9, no. 4, pp. 152–158, 2021, https://doi.org/10.18201/ijisae.2021473633.
- D. Chicco and G. Jurman, “The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation,” BMC Genomics, vol. 21, no. 1, p. 6, 2020, https://doi.org/10.1186/s12864-019-6413-7.
- D. S. Depto, Md. M. Rizvee, A. Rahman, H. Zunair, M. S. Rahman, and M. R. C. Mahdy, “Quantifying imbalanced classification methods for leukemia detection,” Computers in Biology and Medicine, vol. 152, p. 106372, 2023, https://doi.org/10.1016/j.compbiomed.2022.106372.
- V. H. Alves Ribeiro and G. Reynoso-Meza, “Ensemble learning by means of a multi-objective optimization design approach for dealing with imbalanced data sets,” Expert Systems with Applications, vol. 147, p. 113232, 2020, https://doi.org/10.1016/j.eswa.2020.113232.
- A. Altan, “Performance of Metaheuristic Optimization Algorithms based on Swarm Intelligence in Attitude and Altitude Control of Unmanned Aerial Vehicle for Path Following,” in 2020 4th International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), pp. 1–6, 2020, https://doi.org/10.1109/ISMSIT50672.2020.9255181.
- A. Hussain and Y. S. Muhammad, “Trade-off between exploration and exploitation with genetic algorithm using a novel selection operator,” Complex Intell. Syst., vol. 6, no. 1, pp. 1–14, 2020, https://doi.org/10.1007/s40747-019-0102-7.
- Morales-Castañeda, D. Zaldívar, E. Cuevas, F. Fausto, and A. Rodríguez, “A better balance in metaheuristic algorithms: Does it exist?,” Swarm and Evolutionary Computation, vol. 54, p. 100671, 2020, https://doi.org/10.1016/j.swevo.2020.100671.
- R. C. Wilson, E. Bonawitz, V. D. Costa, and R. B. Ebitz, “Balancing exploration and exploitation with information and randomization,” Current Opinion in Behavioral Sciences, vol. 38, pp. 49–56, 2021, https://doi.org/10.1016/j.cobeha.2020.10.001.
- L. Korycki and B. Krawczyk, “Concept Drift Detection from Multi-Class Imbalanced Data Streams,” in 2021 IEEE 37th International Conference on Data Engineering (ICDE), pp. 1068–1079, 2021, https://doi.org/10.1109/ICDE51399.2021.00097.
- W. Liu, H. Zhang, Z. Ding, Q. Liu, and C. Zhu, “A comprehensive active learning method for multiclass imbalanced data streams with concept drift,” Knowledge-Based Systems, vol. 215, p. 106778, 2021, https://doi.org/10.1016/j.knosys.2021.106778.
- S. Priya and R. A. Uthra, “Deep learning framework for handling concept drift and class imbalanced complex decision-making on streaming data,” Complex Intell. Syst., vol. 9, no. 4, pp. 3499–3515, 2023, https://doi.org/10.1007/s40747-021-00456-0.
- W. Grote-Ramm, D. Lanuschny, F. Lorenzen, M. Oliveira Brito, and F. Schönig, “Continual learning for neural regression networks to cope with concept drift in industrial processes using convex optimisation,” Engineering Applications of Artificial Intelligence, vol. 120, p. 105927, 2023, https://doi.org/10.1016/j.engappai.2023.105927.
- P. Li, H. Zhang, X. Hu, and X. Wu, “High-Dimensional Multi-Label Data Stream Classification With Concept Drifting Detection,” IEEE Trans. Knowl. Data Eng., pp. 1–15, 2022, https://doi.org/10.1109/TKDE.2022.3200068.
- H. Mehmood, P. Kostakos, M. Cortes, T. Anagnostopoulos, S. Pirttikangas, and E. Gilman, “Concept Drift Adaptation Techniques in Distributed Environment for Real-World Data Streams,” Smart Cities, vol. 4, no. 1, pp. 349–371, 2021, https://doi.org/10.3390/smartcities4010021.
- S. Ryan, R. Corizzo, I. Kiringa, and N. Japkowicz, “Deep Learning Versus Conventional Learning in Data Streams with Concept Drifts,” in 2019 18th IEEE International Conference On Machine Learning And Applications (ICMLA), pp. 1306–1313, 2019, https://doi.org/10.1109/ICMLA.2019.00213.
- S. Dhivya and R. Arul, “Hybrid Flower Pollination Algorithm for Optimization Problems,” in Proceedings of the International Conference on Computational Intelligence and Sustainable Technologies, pp. 751–762, 2022, https://doi.org/10.1007/978-981-16-6893-7_65.
- P. E. Mergos and X.-S. Yang, “Flower pollination algorithm parameters tuning,” Soft Comput, vol. 25, no. 22, pp. 14429–14447, 2021, https://doi.org/10.1007/s00500-021-06230-1.
- Y. Lu, Y.-M. Cheung, and Y. Y. Tang, “Bayes Imbalance Impact Index: A Measure of Class Imbalanced Data Set for Classification Problem,” IEEE Trans. Neural Netw. Learning Syst., vol. 31, no. 9, pp. 3525–3539, 2020, https://doi.org/10.1109/TNNLS.2019.2944962.
- S. Tyagi and S. Mittal, “Sampling Approaches for Imbalanced Data Classification Problem in Machine Learning,” in Proceedings of ICRIC 2019, vol. 597, pp. 209–221, 2020, https://doi.org/10.1007/978-3-030-29407-6_17.
- A. J. Larrazabal, N. Nieto, V. Peterson, D. H. Milone, and E. Ferrante, “Gender imbalance in medical imaging datasets produces biased classifiers for computer-aided diagnosis,” Proc. Natl. Acad. Sci. U.S.A., vol. 117, no. 23, pp. 12592–12594, 2020, https://doi.org/10.1073/pnas.1919012117.
- T. Liu, W. Fan, and C. Wu, “A hybrid machine learning approach to cerebral stroke prediction based on imbalanced medical dataset,” Artificial Intelligence in Medicine, vol. 101, p. 101723, 2019, https://doi.org/10.1016/j.artmed.2019.101723.
- L. Gao, L. Zhang, C. Liu, and S. Wu, “Handling imbalanced medical image data: A deep-learning-based one-class classification approach,” Artificial Intelligence in Medicine, vol. 108, p. 101935, 2020, https://doi.org/10.1016/j.artmed.2020.101935.
- E. Mortaz, “Imbalance accuracy metric for model selection in multi-class imbalance classification problems,” Knowledge-Based Systems, vol. 210, p. 106490, 2020, https://doi.org/10.1016/j.knosys.2020.106490.
- A. Özdemir, K. Polat, and A. Alhudhaif, “Classification of imbalanced hyperspectral images using SMOTE-based deep learning methods,” Expert Systems with Applications, vol. 178, p. 114986, 2021, https://doi.org/10.1016/j.eswa.2021.114986.
- P. Thölke et al., “Class imbalance should not throw you off balance: Choosing the right classifiers and performance metrics for brain decoding with imbalanced data,” NeuroImage, vol. 277, p. 120253, 2023, https://doi.org/10.1016/j.neuroimage.2023.120253.
- D. Chicco and G. Jurman, “The Matthews correlation coefficient (MCC) should replace the ROC AUC as the standard metric for assessing binary classification,” BioData Mining, vol. 16, no. 1, p. 4, 2023, https://doi.org/10.1186/s13040-023-00322-4.
- Z. Xu, D. Shen, T. Nie, and Y. Kou, “A hybrid sampling algorithm combining M-SMOTE and ENN based on Random forest for medical imbalanced data,” Journal of Biomedical Informatics, vol. 107, p. 103465, 2020, https://doi.org/10.1016/j.jbi.2020.103465.
- G. Kovács, “An empirical comparison and evaluation of minority oversampling techniques on a large number of imbalanced datasets,” Applied Soft Computing, vol. 83, p. 105662, 2019, https://doi.org/10.1016/j.asoc.2019.105662.
- S. Susan and A. Kumar, “The balancing trick: Optimized sampling of imbalanced datasets—A brief survey of the recent State of the Art,” Engineering Reports, vol. 3, no. 4, p. e12298, 2021, https://doi.org/10.1002/eng2.12298.
- A. Ishaq et al., "Improving the Prediction of Heart Failure Patients’ Survival Using SMOTE and Effective Data Mining Techniques,” IEEE Access, vol. 9, pp. 39707–39716, 2021, https://doi.org/10.1109/ACCESS.2021.3064084.
- M. Khushi et al., “A Comparative Performance Analysis of Data Resampling Methods on Imbalance Medical Data,” IEEE Access, vol. 9, pp. 109960–109975, 2021, https://doi.org/10.1109/ACCESS.2021.3102399.
- A. Kishor and C. Chakraborty, “Early and accurate prediction of diabetics based on FCBF feature selection and SMOTE,” Int J Syst Assur Eng Manag, 2021, https://doi.org/10.1007/s13198-021-01174-z.
- V. P. K. Turlapati and M. R. Prusty, “Outlier-SMOTE: A refined oversampling technique for improved detection of COVID-19,” Intelligence-Based Medicine, vol. 3–4, p. 100023, 2020, https://doi.org/10.1016/j.ibmed.2020.100023.
- D. C. E. Saputra, K. Sunat, and T. Ratnaningsih, “A New Artificial Intelligence Approach Using Extreme Learning Machine as the Potentially Effective Model to Predict and Analyze the Diagnosis of Anemia,” Healthcare, vol. 11, no. 5, p. 697, 2023, https://doi.org/10.3390/healthcare11050697.
- X.-S. Yang, “Flower Pollination Algorithm for Global Optimization,” in Unconventional Computation and Natural Computation, vol. 7445, pp. 240–249, 2021, https://doi.org/10.1007/978-3-642-32894-7_27.
- M. Abdel-Basset and L. A. Shawky, “Flower pollination algorithm: a comprehensive review,” Artif Intell Rev, vol. 52, no. 4, pp. 2533–2557, 2019, https://doi.org/10.1007/s10462-018-9624-4.
- X.-S. Yang, M. Karamanoglu, and X. He, “Flower pollination algorithm: A novel approach for multiobjective optimization,” Engineering Optimization, vol. 46, no. 9, pp. 1222–1237, 2014, https://doi.org/10.1080/0305215X.2013.832237.
- Z. A. Abdalkareem, M. A. Al-Betar, A. Amir, P. Ehkan, A. I. Hammouri, and O. H. Salman, “Discrete flower pollination algorithm for patient admission scheduling problem,” Computers in Biology and Medicine, vol. 141, p. 105007, 2022, https://doi.org/10.1016/j.compbiomed.2021.105007.
- M. Abdel-Basset, R. Mohamed, S. Saber, S. Askar, and M. Abouhawwash, “Modified Flower Pollination Algorithm for Global Optimization,” Mathematics, vol. 9, no. 14, p. 1661, 2021, https://doi.org/10.3390/math9141661.
- F. B. Ozsoydan and A. Baykasoglu, “Chaos and intensification enhanced flower pollination algorithm to solve mechanical design and unconstrained function optimization problems,” Expert Systems with Applications, vol. 184, p. 115496, 2021, https://doi.org/10.1016/j.eswa.2021.115496.
- S. Lalljith, I. Fleming, U. Pillay, K. Naicker, Z. J. Naidoo, and A. K. Saha, “Applications of Flower Pollination Algorithm in Electrical Power Systems: A Review,” IEEE Access, vol. 10, pp. 8924–8947, 2022, https://doi.org/10.1109/ACCESS.2021.3138518.
- M. K. Y. Shambour, A. A. Abusnaina, and A. I. Alsalibi, “Modified Global Flower Pollination Algorithm and its Application for Optimization Problems,” Interdiscip Sci Comput Life Sci, vol. 11, no. 3, pp. 496–507, 2019, https://doi.org/10.1007/s12539-018-0295-2.
- Z. A. Alkareem Alyasseri et al., “A hybrid flower pollination with β -hill climbing algorithm for global optimization,” Journal of King Saud University - Computer and Information Sciences, vol. 34, no. 8, pp. 4821–4835, 2022, https://doi.org/10.1016/j.jksuci.2021.06.015.
- N. V. Chawla, K. W. Bowyer, L. O. Hall, and W. P. Kegelmeyer, “SMOTE: Synthetic Minority Over-sampling Technique,” jair, vol. 16, pp. 321–357, 2002, https://doi.org/10.1613/jair.953.
- D. Dablain, B. Krawczyk, and N. V. Chawla, “DeepSMOTE: Fusing Deep Learning and SMOTE for Imbalanced Data,” IEEE Trans. Neural Netw. Learning Syst., vol. 34, no. 9, pp. 6390–6404, 2023, https://doi.org/10.1109/TNNLS.2021.3136503.
- J. M. Johnson and T. M. Khoshgoftaar, “Survey on deep learning with class imbalance,” J Big Data, vol. 6, no. 1, p. 27, 2019, https://doi.org/10.1186/s40537-019-0192-5.
- D. Chicco, M. J. Warrens, and G. Jurman, “The Matthews Correlation Coefficient (MCC) is More Informative Than Cohen’s Kappa and Brier Score in Binary Classification Assessment,” IEEE Access, vol. 9, pp. 78368–78381, 2021, https://doi.org/10.1109/ACCESS.2021.3084050.
- J. Yao and M. Shepperd, “Assessing software defection prediction performance: why using the Matthews correlation coefficient matters,” in Proceedings of the Evaluation and Assessment in Software Engineering, pp. 120–129, 2020, https://doi.org/10.1145/3383219.3383232.
- P. Ferreira, D. C. Le, and N. Zincir-Heywood, “Exploring Feature Normalization and Temporal Information for Machine Learning Based Insider Threat Detection,” in 2019 15th International Conference on Network and Service Management (CNSM), pp. 1–7, 2019, https://doi.org/10.23919/CNSM46954.2019.9012708.
- K. M. Ong, P. Ong, and C. K. Sia, “A new flower pollination algorithm with improved convergence and its application to engineering optimization,” Decision Analytics Journal, vol. 5, p. 100144, 2022, https://doi.org/10.1016/j.dajour.2022.100144.
- M. Ćalasan, S. H. E. Abdel Aleem, and A. F. Zobaa, “On the root mean square error (RMSE) calculation for parameter estimation of photovoltaic models: A novel exact analytical solution based on Lambert W function,” Energy Conversion and Management, vol. 210, p. 112716, 2020, https://doi.org/10.1016/j.enconman.2020.112716.
- S.-H. Tseng and T. Son Nguyen, “Agent-Based Modeling of Rumor Propagation Using Expected Integrated Mean Squared Error Optimal Design,” ASI, vol. 3, no. 4, p. 48, 2020, https://doi.org/10.3390/asi3040048.
- C.-I. Chang, “An Effective Evaluation Tool for Hyperspectral Target Detection: 3D Receiver Operating Characteristic Curve Analysis,” IEEE Trans. Geosci. Remote Sensing, vol. 59, no. 6, pp. 5131–5153, 2021, https://doi.org/10.1109/TGRS.2020.3021671.
- B. Richhariya and M. Tanveer, “A reduced universum twin support vector machine for class imbalance learning,” Pattern Recognition, vol. 102, p. 107150, 2020, https://doi.org/10.1016/j.patcog.2019.107150.
- Y. Zhang, H. Yang, H. Cui, and Q. Chen, “Comparison of the Ability of ARIMA, WNN and SVM Models for Drought Forecasting in the Sanjiang Plain, China,” Nat Resour Res, vol. 29, no. 2, pp. 1447–1464, 2020, https://doi.org/10.1007/s11053-019-09512-6.
- D. Albashish, A. I. Hammouri, M. Braik, J. Atwan, and S. Sahran, “Binary biogeography-based optimization based SVM-RFE for feature selection,” Applied Soft Computing, vol. 101, p. 107026, 2021, https://doi.org/10.1016/j.asoc.2020.107026.
- A. Binbusayyis and T. Vaiyapuri, “Unsupervised deep learning approach for network intrusion detection combining convolutional autoencoder and one-class SVM,” Appl Intell, vol. 51, no. 10, pp. 7094–7108, 2021, https://doi.org/10.1007/s10489-021-02205-9.
- A. Ghavidel and P. Pazos, “Machine learning (ML) techniques to predict breast cancer in imbalanced datasets: a systematic review,” J Cancer Surviv, 2023, https://doi.org/10.1007/s11764-023-01465-3.
- F. Nie, W. Zhu, and X. Li, “Decision Tree SVM: An extension of linear SVM for non-linear classification,” Neurocomputing, vol. 401, pp. 153–159, 2020, https://doi.org/10.1016/j.neucom.2019.10.051.
- G. Aguiar, B. Krawczyk, and A. Cano, “A survey on learning from imbalanced data streams: taxonomy, challenges, empirical study, and reproducible experimental framework,” Mach Learn, Jun. 2023, https://doi.org/10.1007/s10994-023-06353-6.
- P. Gnip, L. Vokorokos, and P. Drotár, “Selective oversampling approach for strongly imbalanced data,” PeerJ Computer Science, vol. 7, p. e604, 2021, https://doi.org/10.7717/peerj-cs.604.
- L. Ju et al., “Hierarchical Knowledge Guided Learning for Real-world Retinal Disease Recognition,” IEEE Trans. Med. Imaging, pp. 1–1, 2023, https://doi.org/10.1109/TMI.2023.3302473.
- N. Liu, X. Li, E. Qi, M. Xu, L. Li, and B. Gao, “A Novel Ensemble Learning Paradigm for Medical Diagnosis With Imbalanced Data,” IEEE Access, vol. 8, pp. 171263–171280, 2020, https://doi.org/10.1109/ACCESS.2020.3014362.
- Z. Xu, D. Shen, T. Nie, Y. Kou, N. Yin, and X. Han, “A cluster-based oversampling algorithm combining SMOTE and k-means for imbalanced medical data,” Information Sciences, vol. 572, pp. 574–589, 2021, https://doi.org/10.1016/j.ins.2021.02.056.
- B. Baesens, S. Höppner, I. Ortner, and T. Verdonck, “robROSE: A robust approach for dealing with imbalanced data in fraud detection,” Stat Methods Appl, vol. 30, no. 3, pp. 841–861, 2021, https://doi.org/10.1007/s10260-021-00573-7.
- T. C. Tran and T. K. Dang, “Machine Learning for Prediction of Imbalanced Data: Credit Fraud Detection,” in 2021 15th International Conference on Ubiquitous Information Management and Communication (IMCOM), pp. 1–7, 2021, https://doi.org/10.1109/IMCOM51814.2021.9377352.
- C. A. Brosey and J. A. Tainer, “Evolving SAXS versatility: solution X-ray scattering for macromolecular architecture, functional landscapes, and integrative structural biology,” Current Opinion in Structural Biology, vol. 58, pp. 197–213, 2019, https://doi.org/10.1016/j.sbi.2019.04.004.
- A. Khraisat and A. Alazab, “A critical review of intrusion detection systems in the internet of things: techniques, deployment strategy, validation strategy, attacks, public datasets and challenges,” Cybersecur, vol. 4, no. 1, p. 18, 2021, https://doi.org/10.1186/s42400-021-00077-7.
AUTHOR BIOGRAPHY

| Dimas Chaerul Ekty Saputra is received his bachelor’s degree from the Department of Informatics, Faculty of Industrial Technology, Ahmad Dahlan University, Yogyakarta, Indonesia in 2020, an M.Sc. degree in Department of Biomedical Engineering, Graduate School, Universitas Gadjah Mada, Yogyakarta, Indonesia in 2022, and now he is a PhD candidate in the Department of Computer Science, College of Computing, Khon Kaen University, Khon Kaen, Thailand. He is currently a lecturer at Telkom University Surabaya, Indonesia. He is also a member of the Association for Scientific Computing and Electronics, Engineering (ASCEE) Student Branch Indonesia. His research interests include artificial Intelligence, pattern recognition, machine learning, signal processing, and bioinformatics. |
|
|

| Tri Ratnaningsih is received the Medical Doctor degree from the Faculty of Medicine, Gadjah Mada University, Indonesia, in 1995, and the master's degree in tropical medical science and the Ph.D. degree in health science from Gadjah Mada University. Subsequently, she continued her career as Clinical Pathologist and became a Hematology and Transfusion Medicine consultant, in 2014. She is currently a Lecturer and holds the position of Head of the Department of Clinical Pathology and the Laboratory Medicine, Universitas Gadjah Mada, Indonesia. |
|
|

| Irianna Futri is received her Bachelor's degree in Information Systems from the Nurdin Hamzah School of Computer and Informatics Management in Jambi, Indonesia, in 2011. She worked at The Construction Services Public Works Department Jambi for 1 year as an Administrator for SIPJAKI (Construction Services Development Information System). She also worked as an informatics teacher at Vocational School of Dharma Bhakti 4 for 3 years and served as an Operator for Dapodik for 7 years. Currently, she is pursuing a Master's degree in International Technology and Innovation Management at the International College, Khon Kaen University, Khon Kaen, Thailand. Her current research interests include advanced care plans and bibliometric analysis. |
|
|

| Elvaro Islami Muryadi is received his bachelor’s degree in public health, Respati Indonesia University, Jakarta, Indonesia, in 2015. Prior to that, in 2023, he completed a master's program in public health at Prima Indonesia University, Medan, Indonesia, after completing a master's program in business administration at Respati Indonesia University, Jakarta, Indonesia, in 2018. At present, he is engaged in doctoral studies at Khon Kaen University, Thailand, Faculty of Medicine, Department of Community, Occupational, and Family Medicine. Health education, public health, health promotion, and family medicine are among his current research interests. |
|
|

| Raksmey Phann is received his M.Sc. degree in Data Science and Artificial Intelligence, Khon Kaen University, Khon Kaen 40002, Thailand, in 2023, and now he is a lecturer in the Department of Applied Mathematics and Statistics, Institute of Technology of Cambodia, Phnom Penh 120408, Cambodia. His research interests include artificial intelligence, natural language processing, machine learning, speech synthesis, text classification, and computer vision. |

| Su Sandi Hla Tun is received her Bachelor's degree in Physiotherapy from University of Medical Technology, Yangon, Myanmar in 2010, master’s degree in Physiotherapy from University of Medical Technology, Yangon, Myanmar in 2018, Diploma of Research Studies from Yangon University, Myanmar in 2020. She worked as a Project Officer in The Leprosy Mission Myanmar for 1 year. She also worked as a tutor in Department of Physiotherapy, University of Medical Technology, Yangon, Myanmar for 7 years. Currently, she is pursuing a Ph. D. degree in Human Movement Sciences, Faculty of Associated Medical Sciences, Khon Kaen University, Khon Kaen, Thailand. Her current research interests are neurorehabilitation, pediatric rehabilitation and biostatistics. Her research projects are rehabilitation of patients with stroke in their activities and quality of life. |

| Ritchie Natuan Caibigan is received his B.S. degree in Computer Science, Cum Laude, from the Lyceum of the Philippines University – Batangas, Philippines in 2022. He was awarded Top 4 Sotero H. Laurel Outstanding Student for his campaigns for national computer literacy by being one of the convenors of a program that delivers software packages under the Information and Computer Technology (ICT) track. Mr. Caibigan served as a lecturer in Batangas State University – The Philippine Engineering University. He is currently pursuing a M.Sc. degree in Computer Science and Information Technology, Khon Kaen University, Khon Kaen, Thailand. His research interests include data mining, graph neural network, ensemble learning, and recommender systems. |
HNIHA: Hybrid Nature-Inspired Imbalance Handling Algorithm to Addressing Imbalanced Datasets for Improved Classification: In Case of Anemia Identification (Dimas Chaerul Ekty Saputra)