A mathematical model of meningitis with antibiotic effects
DOI:
https://doi.org/10.12928/bamme.v3i1.9475Keywords:
basic reproduction number, global stability, local stability, meningitisAbstract
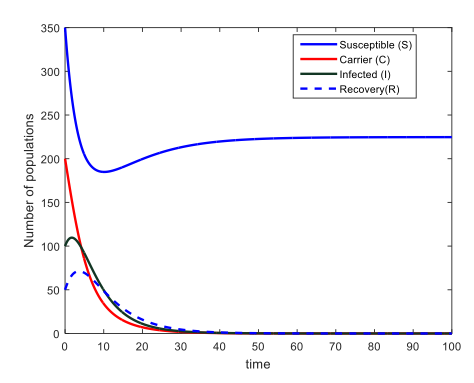
The mathematical model in this study is a SCIR-type meningitis disease spread model, namely susceptible (S), carrier (C), infected (I), and recovery (R). In the model used, there are two equilibrium points, namely the disease-free equilibrium point and the endemic equilibrium point. The conditions and stability of the equilibrium point are determined by the basic reproduction number, which is the value that determines whether or not the spread of meningitis infection in a population. The results of this study show that the stability of the disease-free equilibrium point and the endemic equilibrium point are locally asymptotically stable and by using the Lyapunov Function method it is found that the disease-free equilibrium point will be globally stable when, while the endemic equilibrium point will be globally stable when numerical simulations perform to support the theoretical results.
References
Afifah, I., Helmi, & Noviani, E. (2019). Analisis kestabilan global model penyebaran penyakit meningitis dengan menggunakan fungsi Lyapunov. Bimaster: Buletin Ilmiah Matematika, Statistika Dan Terapannya, 8(4), 829–838.
Asamoah, J. K. K., Nyabadza, F., Seidu, B., Chand, M., & Dutta, H. (2018). Mathematical modelling of bacterial meningitis transmission dynamics with control measures. Hindawi: Computational and Mathematical Methods in Medicine, 1-21.
Asamoah, J. K. K., Nyabadza, F., Jin, Z., Bonyah, E., Khan, M. A., Li, M. Y., & Hayat, T. (2020). Backward bifurcation and sensitivity analysis for bacterial meningitis transmission dynamics with a nonlinear recovery rate. Chaos, Solitons and Fractals, 140, 1-16.
Hadning, I., Endarti, D., Andayani, T. M., & Triasih, R. (2020). Cost of illness of inpatient pediatric meningitis patients hospitalized in yogyakarta. Jurnal Farmasi Sains dan Praktis, 6(1), 9-18.
Hardiyanti, M. P., Isnanto, R. R., & Windasari, I. P. (2017). Aplikasi sistem pakar berbasis mobile untuk diagnosis dini meningitis. Jurnal Teknologi dan Sistem Komputer, 5(2), 84-89.
Kotola, B. S., Mekonnen, T. T. (2022). Mathematical model analysis and numerical simulation for codynamics of meningitis and pneumonia infection with intervention. Science Report, 12(2639). https://doi.org/10.1038/s41598-022-06253-0
Martcheva, M. (2013). An introduction to mathematical epidemiology. Springer.
Olsder, G. J. (1994). Mathematical Systems Theory. Delft University Press.
Peter, O. J., Yusuf, A., Ojo, M. M. (2002). A mathematical model analysis of meningitis with treatment and vaccination in fractional derivatives. International Journal of Applied Computing Mathematics, 8(117). https://doi.org/10.1007/s40819-022-01317-1
Shan, C., & Zhu, H. (2014). Bifurcations and complex dynamics of an SIR model with the impact of the number of hospital beds. Journal of Differential Equations, 257(5), 1662–1688.
Sheehan J. (2009). Using antibiotics to treat meningitis. https://www.everydayhealth.com/meningitis/using-antibiotics-to-treat-meningitis.aspx
Türkün, C., Gölgeli, M. & Atay, F.M. (2023). A mathematical interpretation for outbreaks of bacterial meningitis under the effect of time-dependent transmission parameters. Nonlinear Dynamic, 111, 14467–14484. https://doi.org/10.1007/s11071-023-08577-6
Van den Driessche, P., & Watmough, J. (2002). Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences, 180, 29-48.
Vargas de León, C. (2009). Constructions of Lyapunov functions for classics SIS, SIR and SIRS epidemic model with variable population size. Foro-Red-Mat: Revista Electrónica de Contenido Matemático, 26(5), 1-12.
Yanuar, W., Sari, I. P., & Nuryastuti, T. (2019). Evaluasi terapi antibiotik empirik terhadap clinical outcome pada pasien anak dengan meningitis bakteri di bangsal rawat inap RSUP Dr. Sardjito Yogyakarta 2010-2015. Majalah Farmaseutik, 14(2), 49.
Downloads
Published
Issue
Section
License
Copyright (c) 2023 Yudi Ari Adi

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Authors who publish with this journal agree to the following terms:
- Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under Creative Commons Attribution License that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
- Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.
- Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See The Effect of Open Access).



