Optimal control on education, vaccination, and treatment in the model of dengue hemorrhagic fever

Authors

  • Eva Annisa Haafidhoh Universitas Ahmad Dahlan
  • Yudi Ari Adi Universitas Ahmad Dahlan
  • Nursyiva Irsalinda Universiti Malaysia Terengganu

DOI:

https://doi.org/10.12928/bamme.v2i2.7617

Keywords:

SEIR epidemic model, Dengue hemorrhagic fever, Optimal control, Pontryagin minimum principle

Abstract

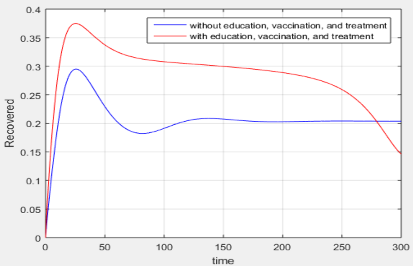
Dengue hemorrhagic fever (DHF) is an infection caused by the dengue virus which is transmitted by the Aedes aegypti mosquito. In this paper, a model of the spread of dengue disease is developed using optimal control theory by dividing the population into Susceptible, Exposed, Infected, and Recovered (SEIR) sub-populations. The Pontryagin minimum principle of the fourth-order Runge-Kutta method is used in the model of the spread of dengue disease by incorporating control factors in the form of education and vaccination of susceptible human populations, as well as treatment of infected human populations. Optimum control aims to minimize the infected human population in order to reduce the spread of DHF. Simulations were carried out for two cases, namely when the basic reproduction number   is less than one for disease-free conditions and  greater than one for endemic conditions. Based on numerical simulations of the SEIR epidemic model with controls, it results that the optimal strategy is achieved if education controls, vaccinations, and medication are used.

References

Chamnan, A., Pongsumpun, P., Tang, I., & Wongvanich, N. (2021). Local and Global Stability Analysis of Dengue Disease with Vaccination and Optimal Control. 13, 1–24.

Dania, I. A. (2016). Gambaran Penyakit dan Vektor Demam Berdarah Dengue (DBD). Majalah Ilmiah

Warta Dharmawangsa, Edisi 48, 1–14.

Dorigatti, I., Aguas, R., Donnelly, C. A., Guy, B., Coudeville, L., Jackson, N., Saville, M., & Ferguson, N. M. (2015). Modelling the immunological response to a tetravalent dengue vaccine from multiple phase-2 trials in Latin America and South East Asia. Vaccine, 33(31), 3746–3751. https://doi.org/10.1016/j.vaccine.2015.05.059

Iin, N. K., Yulianti, D. L., Luron, N. G., Pomalingo, S. F., Noviana, W., & Hidaya, N. (2020). Keterkaitan Antara Kondisi Lingkungan Dan Perilaku Masyarakat Terhadap Keberadaan Vektor Demam Berdarah Dengue (DBD). Journal of Borneo Holistic Health, 3(2), 75–85. https://doi.org/10.35334/borticalth.v3i2.1506

Ministry of Health. (2017). Situasi Penyakit Demam Berdarah di Indonesia Tahun 2017 (pp. 1–7).

Khan, M. A., & Fatmawati. (2021). Dengue infection modeling and its optimal control analysis in

East Java, Indonesia. Heliyon, 7, e06023. https://doi.org/10.1016/j.heliyon.2021.e06023

Onyejekwe, O. O., Tigabie, A., Ambachew, B., & Alemu, A. (2019). Application of Optimal Control to the Epidemiology of Dengue Fever Transmission. 7, 148–165. https://doi.org/10.4236/jamp.2019.71013

Sabran, L. O., & Jannah, M. (2020). Model Matematika SEIRS-SEI pada Penyebaran Penyakit Demam

Berdarah Dengue dengan Pengaruh Suhu. MAP, 66–78.

Sethi, S. P. (2019). What Is Optimal Control Theory? Optimal Control Theory, 1–26.

https://doi.org/10.1007/978-3-319-98237-3_1

Windawati, S., Shodiqin, A., & Aini, A. N. (2020). Analisis Kestabilan Model Matematika Penyebaran

Penyakit Demam Berdarah dengan Pengaruh Fogging. 2(1), 1–16.

Downloads

Published

2023-02-04

Issue

Vol. 2 No. 2 (2022)

Section

Articles

License

Copyright (c) 2022 Eva Annisa Haafidhoh, Yudi Ari Adi, Nursyiva Irsalinda

Creative Commons License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Authors who publish with this journal agree to the following terms:

  1. Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under a Creative Commons Attribution License that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
  2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.
  3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See The Effect of Open Access).