Simulating Bitcoin price movements with the Bates model and Monte Carlo methods
DOI:
https://doi.org/10.12928/bamme.v5i1.12815Keywords:
Bates model, Bitcoin simulation, Jump-Diffusion, Monte Carlo methods, Stochastic volatilityAbstract
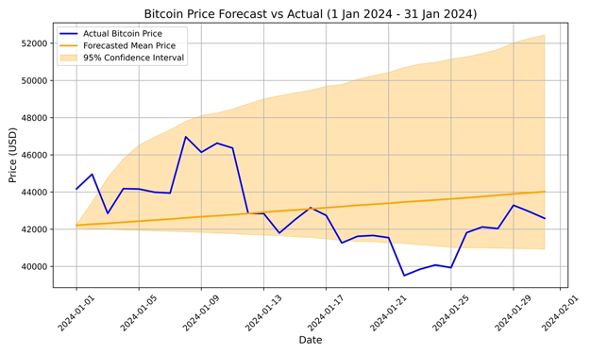
This study investigates the price dynamics of Bitcoin, a highly volatile and speculative digital asset. Using daily closing price data from January 2023 to January 2024, we apply the Bates model, which combines stochastic volatility with jump-diffusion processes, to better capture both continuous fluctuations and sudden, large price changes in the market. The model parameters are calibrated using historical data and evaluated through Monte Carlo simulation with 10,000 generated price paths over a 31-day forecast horizon. The results demonstrate a strong short-term predictive performance, with a Mean Absolute Percentage Error (MAPE) of 4.32%. This indicates that the Bates model can capture both volatility clustering and abrupt shifts, which are characteristic of Bitcoin. The findings suggest that this approach provides a valuable tool for risk management and investment decision-making in highly uncertain and dynamic markets.
References
AlMadany, N. N., Hujran, O., Naymat, G. Al, & Maghyereh, A. (2024). Forecasting cryptocurrency returns using classical statistical and deep learning techniques. International Journal of Information Management Data Insights, 4(2). https://doi.org/10.1016/j.jjimei.2024.100251
Brini, A., & Lenz, J. (2024). A comparison of cryptocurrency volatility-benchmarking new and mature asset classes. Financial Innovation, 10(1). https://doi.org/10.1186/s40854-024-00646-y
Chen, Y., Zhang, L., & Bouri, E. (2024). Can a self-exciting jump structure better capture the jump behavior of cryptocurrencies? A comparative analysis with the S&P 500. Research in International Business and Finance, 69, 102277. https://doi.org/https://doi.org/10.1016/j.ribaf.2024.102277
Chiarella, C., He, X. Z., & Nikitopoulos, C. S. (2015). Ito’s Lemma and Its Applications. In Derivative Security Pricing: Techniques, Methods and Applications (pp. 111–143). Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-45906-5_6
Kim, J. M., Jun, C., & Lee, J. (2021). Forecasting the volatility of the cryptocurrency market by garch and stochastic volatility. Mathematics, 9(14). https://doi.org/10.3390/math9141614
Levendis, A. (2023). On the calibration of stochastic volatility models to estimate the real-world measure used in option pricing. ORION, 39(1). https://doi.org/10.5784/39-1-747
Levental, S., Schroder, M., & Sinha, S. (2013). A simple proof of functional Itô’s lemma for semimartingales with an application. http://ssrn.com/abstract=2266460
Narayan, S., & Kumar, D. (2024). Unveiling interconnectedness and risk spillover among cryptocurrencies and other asset classes. Global Finance Journal, 62, 101018. https://doi.org/https://doi.org/10.1016/j.gfj.2024.101018
Petropoulos, F., Apiletti, D., Assimakopoulos, V., Babai, M. Z., Barrow, D. K., Ben Taieb, S., Bergmeir, C., Bessa, R. J., Bijak, J., Boylan, J. E., Browell, J., Carnevale, C., Castle, J. L., Cirillo, P., Clements, M. P., Cordeiro, C., Cyrino Oliveira, F. L., De Baets, S., Dokumentov, A., … Ziel, F. (2022). Forecasting: theory and practice. International Journal of Forecasting, 38(3), 705–871. https://doi.org/https://doi.org/10.1016/j.ijforecast.2021.11.001
Rustamov, O. V. (2024). Understanding volatility in financial markets: A roadmap for risk management and opportunity identification. International Journal of Innovative Technologies in Economy, 2(46). https://doi.org/10.31435/rsglobal_ijite/30062024/8168
Sene, N. F., Konte, M. A., & Aduda, J. (2021). Pricing Bitcoin under double exponential jump-diffusion model with asymmetric jumps stochastic volatility. Journal of Mathematical Finance, 11(02), 313–330. https://doi.org/10.4236/jmf.2021.112018
Sharif, S. V., Parker, D. C., Waddell, P., & Tsiakopoulos, T. (2023). Understanding the effects of market volatility on profitability perceptions of housing market developers. Journal of Risk and Financial Management, 16(10). https://doi.org/10.3390/jrfm16100446
Singh, A., Jha, A. K., & Kumar, A. N. (2024). Prediction of Cryptocurrency Prices through a Path Dependent Monte Carlo Simulation. http://arxiv.org/abs/2405.12988
Wati, E., Dacesta Barus, R., Aini, N., Nugroho, B., & Fauzi, R. (2024). Modeling bitcoin price by using Euler-Maruyama method. Journal of Actuarial, 3(1). http://e-journal.president.ac.id/presunivojs/index.php/JAFRM/index38
Downloads
Published
Issue
Section
License
Copyright (c) 2025 Staenly, Maria Yus Trinity Irsan

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Authors who publish with this journal agree to the following terms:
- Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under Creative Commons Attribution License that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
- Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.
- Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See The Effect of Open Access).



